无监督学习(Chap.9-11)

复制本地路径 | 在线编辑

无监督学习，就是不要标签

K-Means 算法

分类问题，这个太简单了，直接网上搜一下视频即可。

EM 算法

用来做什么: 用于预测概率问题
这里我感觉 CS229 上面太晦涩了，上来就是什么高斯混合模型。李航老师那本统计学习方法挺好。

基本思想

先看一下《统计学习方法》的第一节，也就是三硬币模型，主要就是知道 EM 他也是这种迭代计算的方式。
然后看《统》中的第三节，关于高斯混合模型的介绍，不需要看之后在其上面使用 EM 算法的推到，直接看结果，会发现其实也是对参数进行优化迭代。但是要注意：不要想着之前的三硬币模型！
然后就看一下 CS229 上面的章节，它一开始就讲了高斯混合模型。这里注意的是，两个地方对高斯混合模型的定义有点不同，但都是对的，只不过 CS229 用的是协方差矩阵。
然后回顾三硬币模型，为什么说在看高斯混合模型时不要去想它呢，因为三硬币模型并不是高斯混合模型。其实这也说明：EM 算法并不局限在高斯混合模型，这也是为什么我觉得 CS229 有点晦涩了。

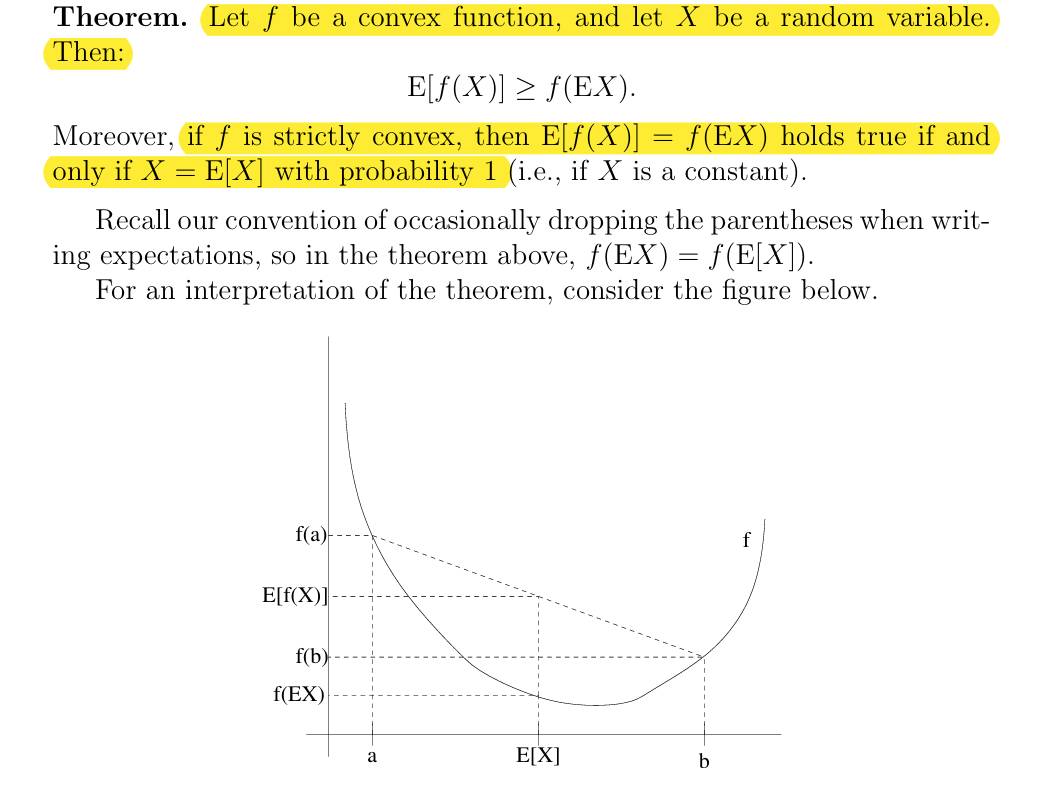
Jensen's inequality

直接看 CS229 的凸函数图像例子，要明白证明是非常学术和复杂的，所以这里的图形化只是说明其中的某一种情况。不要纠结于证明，这个例子只是用来便于记忆这个不等式。

PCA & SVD

PCA 建议看这篇文章，完美: 链接

SVD 建议看这篇文章: 链接

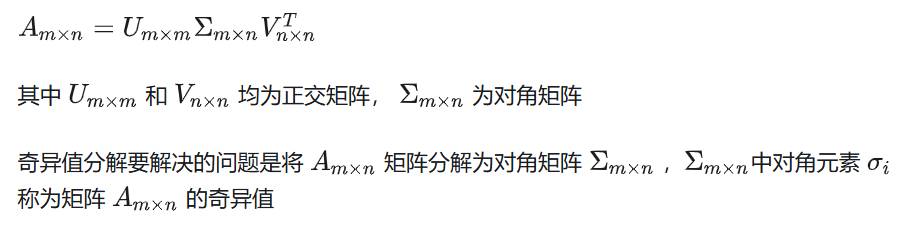
其实重点是这两是干嘛的？这两区别和用途是什么：
1. PCA 常用于降维，便于加快之后的处理。
2. SVD 常用于压缩，SVD 分解后得到一系列奇异值，排好序。压缩就是只保留前多少个奇异值，因为前面几个奇异值已经表示了绝大部分内容。也可以用于降噪，因为认为前面几个大的奇异值已经表示了低频信息。
3. PCA 和 SVD 的联系: 其实可以理解为 PCA 是 SVD 的子集，PCA 在一些库的实现方式就是通过 SVD 来完成的！（因为这样更快更好）
4. 更进一步的理解: PCA 与 SVD 的右奇异向量的压缩效果相同。

ICA 算法

这里 CS229 讲的一般。但是也没有找到比较好的其他资料。
1. ICA 是干嘛的，知道这个例子: d 个人讲话，d 个话筒记录，怎么把它们分离呢？这个场景很常见，比如医学里面的各种电图，就是多个电图的组合，如何分离就是个重要问题。
2. 然后就按照 CS229 看吧，感觉耐心点也可以。