Skip to content

回归问题(Chap.1-3)

复制本地路径 | 在线编辑

回顾问题是最简单的开始。首先是预测，也是最简单的线性回归；然后是分类，也是比较简单的逻辑回归。

这里直接看 CS229 即可，但不需要细看，直接以公式为跳板往下看。下面就是简单的一些问题记录。

  1. 对参数进行迭代预测时，有两种方法: stochastic gradient descent 和 batch gradient descent，直接看 CS229 的公式即可。之后直接转成了向量格式直接可以获取结果，即 1.2 最后的公式:

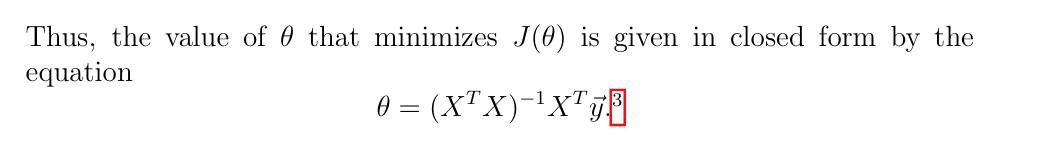
  1. 提出了一个问题: Why least squares?，从而引入极大似然度，直接看 1.3 即可，结论就是：这相当于最大化极大似然度。

  1. 然后很完美了？不是，\(X^TX\)要是可逆的，有时候可不是哦。所以有了牛顿法，在 2.3 之中。对于牛顿法需要理解如下:
    • 要理解它是什么: 记住 \(f'\) 是斜率，这个视频极好！
    • 它如何用在回归函数上: 目标是最大化 \(l(t)\)，即目标是 \(l'(t) = 0\)，那么令 \(f(t) = l'(t)\) 这不就 OK 了
    • 评价梯度下降和牛顿法的优缺点: 2.3 最后的一段话很棒，一般而言牛顿法更快，取决于 Hessian 矩阵的大小:

  1. 有一个概念 locally weighted regression，1.4 讲的，但其实就是加窗，只考虑该点附近的数据。包括不同的窗口：平均、高斯...

  2. 有一个概念 perceptron learning algorithm，2.2 讲了这个，就记住概念就好，没什么用。

  1. 有一个概念 softmax regression，查阅 Page33 看概念，实际就是二维问题的扩展呗，y 不局限 0 or 1，而是 0-k

  1. 最后引入了 Generalized linear models (GLM)，这个 CS229 讲的很好，当然不要太费精力看这个。就知道这个相当于是构建了一个总体的模型，之前所说的线性回归、逻辑回归、softmax 都符合这个模型。

  2. 其实我觉得很有必要学习一下优化的知识，这些概念 L1/L2 范数、岭回归、LASSO 问题...

Comments