梯度下降和共轭梯度下降

最优化中的基础内容。梯度下降，机器学习基础中的基础知识，这个在CS229中学过，当时觉得很简单啊。但是现在来看，还是缺少理解，导致后续对共轭梯度下降的学习产生了阻碍。而共轭下降则是求解线性方程组常用的一个方法。

还是强调一句：学以致用，其实会用就可以了，记录梯度下降和共轭梯度下降的原理是我在阅读论文时（一篇融合闪光和非闪光图像的论文）遇到了麻烦，特此记录。

本文章主要参考了两个网页内容，这两个网页写的非常好！

• https://o-o-sudo.github.io/numerical-methods/-conjugate-gradient.html
• https://pynumerical.com/archives/88/ and https://pynumerical.com/archives/89/

从梯度下降说起

什么！梯度下降还要讲吗？虽然没必要，但我觉得两点是需要理解的：梯度下降为什么能解决Ax=b，梯度下降中每一步之间的关系是什么。

第一个问题，梯度下降为什么解决了Ax=b，实际上他不是直接对Ax-b进行求解，而是很巧妙地转换为了求一个二次函数最小值。求出最小值，我们就获得了最后的解x。

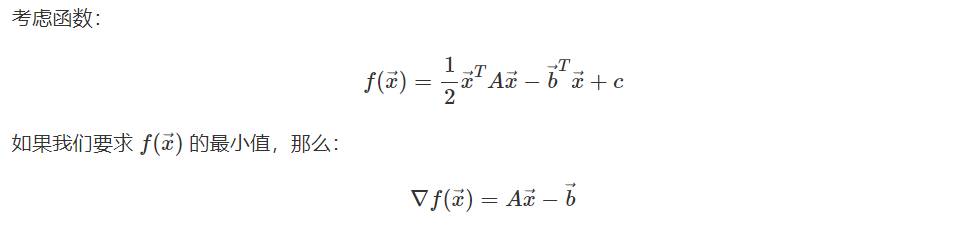
求最小值我们就可以逐步迭代去求，根据公式推导推出形式化解法，也就是令梯度下降方法从而得出。

那么第二个问题，梯度下降中每一步之间的关系是什么。实际上上一张图公式8那儿已经给了答案：前后两步梯度向量保证正交！！在图像中就是下图。绿线就是梯度下降，他每次保证是正交的，所以可能：原来一个方向已经到了最优解，结果现在去求第二个方向最优解，导致之前的方向又不是最优的了，所以会反反复复，导致速度变慢。

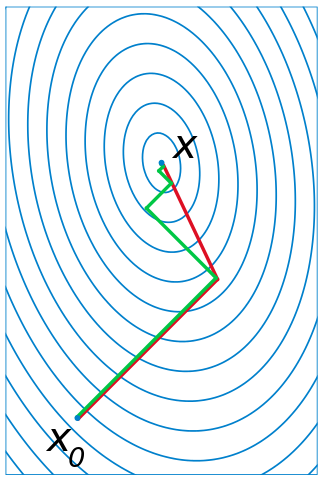
共轭梯度下降

共轭梯度下降可以达到上图红线的效果。而它的推导过程如下，本部分完全记录于 https://pynumerical.com/archives/89/，非常好的文章。

Comments