Guided Filtering的开端

一. 前言

我准备在工作闲暇之余写一些有用的图像处理算法。以前很少系统的写一个小方向的开端、发展以及最新成果，所以我在这儿挖了第一个坑，名字叫做《Guided Filtering的开端与发展》。本篇是第一章，Guided Filtering的开端。

二. 背景

引导滤波器（Guided Filtering）是10年由何凯明大神和旷视已故研究院院长孙剑写的一篇滤波方向的论文，这里缅怀一下孙剑老师（R.I.P.）。如今，就算深度学习方法大行其道，Guided Filtering还是能在图像降噪、平滑、HDR、上采样、去雾以及图像保边等方向应用广泛。

本篇想从：

1）提出guided filter的原因；

2）公式推导；

3）代码讲解；

3个方面讲解Guided Filter。

三. guided filter方法

3.1 提出guided filter的原因

问题：现在有一张下图（左）的原始图像，希望通过算法处理后的图像如右图一样，在脸部平坦区域尽可能的平滑光亮、突出区域（如眉毛、眼镜、发丝）等尽可能锐利。

解决方法：

双边滤波器（Bilateral Filter），应该是当时最流行的一种保边平滑滤波器，它的最主要的思想是在空间距离和颜色强度距离上构建kernel。

但是 双边滤波器致命的缺点 是：

1）边缘处容易发生梯度反转伪影；

2）运行时间太长（尽管后续有一些在双边空间上滤波的快速解决方法）；

为了解决上面双边滤波器的问题，作者提出的引导滤波器。

3.2 guided filter

3.2.1 介绍

引导滤波器方法是一种基于优化算法，所谓优化算法一般都有一个特定的公式，就是：构建一个能量函数，通过一种优化策略使得能力函数最小化。通常被定义为：

$E = U + V$ E = U + V

其中，U是数据项，V是平滑项。构建完能量函数之后，通过一些如最小二乘法、马尔可夫随机场、回归等方法使得能量函数E最小。

相对于第一步，第二步往往是一些矩阵求解。其实最难的是第一步，构建能量函数。

3.2.2 引导滤波的能量函数

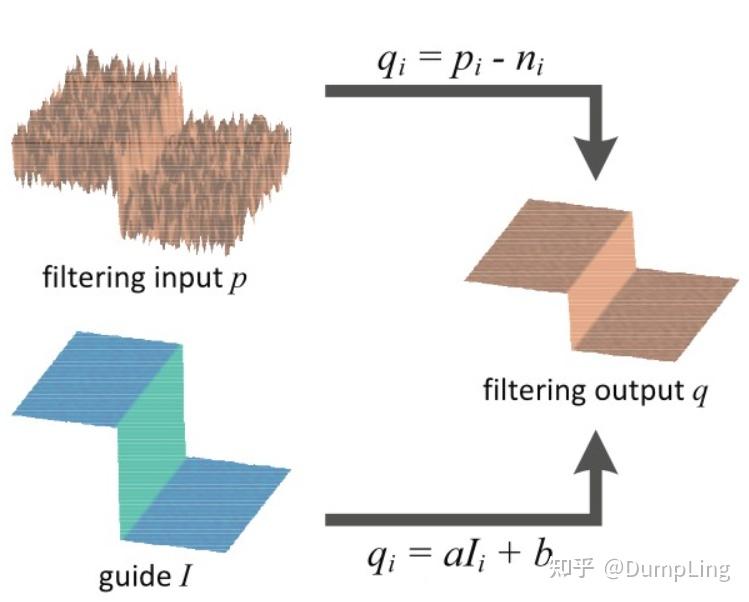
首先，为什么叫引导滤波，因为它其实是输入了两张图：一张引导图像 I、一张要被处理的输入图像 p，如下图所示。为了简单起见，这里的两张图像都是同一张图像。

这张图表达的非常清晰了，就是通过引导图像I对输入的图像p 进行保边平滑，即输出图像q边缘像引导图的边缘，梯度较小的区域像引导图一样平坦。

能量函数：

引导滤波的一个重要假设是输出图像q和引导图像I在局部窗口 k x k 上存在局部线性关系：

$\begin{matrix} (1) & q_{i} = a_{k} I_{i} + b_{k}, \forall i \in ω_{k}, \end{matrix}$ q_{i}=a_{k}I_{i}+b_{k},\forall i\in\omega_{k},\tag {1}

其中，(ak, bk)是一个 k x k 窗口内唯一的常量线性系数。也就是说k x k 窗口只有一个ak和bk。这就保证了在一个局部区域里，如果引导图像I 有一个边缘的时候，输出图像q 也保持边缘不变，因为对于相邻的像素点而言，存在 $\nabla q = a \nabla I$ ∇q = a ∇ I ；而输入图像中非边缘区域又不平滑的区域视为噪声n，就有 $q_{i} = p_{i} - n_{i}$ q _i = p_ i − n_ i ，如图3所示。

这样，保边和平滑都定义出来了。为了最小化噪声，能量函数被定义为：

$\begin{matrix} (2) & E = \sum_{i \in ω_{k}} ((q_{i} - p_{i})^{2}) . \end{matrix}$ E=\sum_{i\in\omega_{k}}((q_i-p_{i})^{2}).\tag {2}

由公式（1）可得：

$\begin{matrix} (3) & E (a_{k}, b_{k}) = \sum_{i \in ω_{k}} ((a_{k} I_{i} + b_{k} - p_{i})^{2}) . \end{matrix}$ E(a_{k},b_{k})=\sum_{i\in\omega_{k}}((a_{k}I_{i}+b_{k}-p_{i})^{2}).\tag {3}

再加上平滑项，最终的能量函数被定义为：

$\begin{matrix} (4) & E (a_{k}, b_{k}) = \sum_{i \in ω_{k}} ((a_{k} I_{i} + b_{k} - p_{i})^{2} + ϵ a_{k}^{2}) . \end{matrix}$ E(a_{k},b_{k})=\sum_{i\in\omega_{k}}((a_{k}I_{i}+b_{k}-p_{i})^{2}+\epsilon a_{k}^{2}).\tag {4}

其中ϵ是一个常数，用于避免ak过大。

从公式（4）可以看到，能量函数只有ak和bk两个未知数，而式（4）又是很简单的二元二次函数；我们知道二次函数最小值可以通过求导，导数为0的点就是最小值点。这样就把式（4）的求解看成最小二乘问题了。

先让式（4）对bk求偏导（因为求bk简单一点）可得：

$\begin{matrix} (5) & \frac{δ E}{b_{k}} = \sum_{i \in ω_{k}} (2 ({a_{k} I}_{i} + b_{k} - p_{i})) = 0; \end{matrix}$ \frac{\mathrm{{\delta E}}}{\mathrm{{b}}_{\mathrm{{k}}}}=\sum_{\mathrm{i{\in}\omega_{\mathrm{{k}}}}}(2(\mathrm{{a_{k}I}}_{\mathrm{{i}}}+\mathrm{{b_{k}-p_{\mathrm{{i}}}}}))=0;\tag {5}

那么bk就等于：

$\begin{matrix} (6) & b_{k} = \frac{1}{| ω |} (\sum_{i \in ω_{k}} p i - a_{k} \sum_{i \in ω_{k}} I_{i}) \end{matrix}$ \mathrm{b_{k}}=\frac{1}{\vert{\bf \omega}\vert}\bigl(\sum_{\mathrm{i{\in}\omega_{k}}}{\bf p}\mathrm{i}-\mathrm{a}_{\bf k}\sum_{\mathrm{i{\in}\omega_{k}}}I_{\mathrm{i}}\bigr)\tag {6}

其中，ω是窗口内的像素个数。记： $\bar{p_{k}} = \frac{1}{| ω |} \sum_{i \in ω_{k}} p i, \bar{I_{k}} = \frac{1}{| ω |} \sum_{i \in ω_{k}} I_{i}$ \overline{p_k}=\frac{1}{\vert{\bf \omega}\vert}\sum_{\mathrm{i{\in}\omega_{k}}}{\bf p}\mathrm{i}\,,\,\,\overline{\mathrm{I_k}}=\frac{1}{\vert{\bf \omega}\vert}\sum_{\mathrm{i{\in}\omega_{k}}}{ I_i} ；则式（6）简化为：

$\begin{matrix} (7) & b_{k} = \bar{p_{k}} + a_{k} \bar{I_{k}} \end{matrix}$ b_k = \overline{p_k} + a_k\overline{I_k} \tag {7}

然后对ak求偏导：

$\begin{matrix} (8) & \frac{δ E}{a_{k}} = \sum_{i \in ω_{k}} (a_{k} I_{i}^{2} + b_{k} I_{i} - p_{i} I_{i} + ε a_{k}) = 0; \end{matrix}$ \frac{\mathrm{{\delta E}}}{\mathrm{{a}}_{\mathrm{{k}}}}=\sum_{\mathrm{i{\in}\omega_{\mathrm{{k}}}}}(a_kI_i^2 + b_kI_i - p_iI_i + \varepsilon a_k)=0;\tag {8}

简化一下：

$\begin{matrix} (9) & \sum_{i \in ω_{k}} (a_{k} I_{i}^{2} + (\bar{p_{k}} + a_{k} \bar{I_{k}}) I_{i} - p_{i} I_{i} + ε a_{k}) = 0; \end{matrix}$ \sum_{\mathrm{i{\in}\omega_{\mathrm{{k}}}}}(a_kI_i^2 + (\overline{p_k} + a_k\overline{I_k})I_i - p_iI_i + \varepsilon a_k)=0;\tag {9}

$\begin{matrix} (10) & a_{k} \sum_{i \in ω_{k}} (I_{i}^{2} + \bar{I_{k}} I_{i} + ε) = \sum_{i \in ω_{k}} (p_{i} I_{i} + \bar{p_{k}} I_{i}); \end{matrix}$ a_k\sum_{\mathrm{i{\in}\omega_{\mathrm{{k}}}}}(I_i^2 + \overline{I_k}I_i + \varepsilon )=\sum_{\mathrm{i{\in}\omega_{\mathrm{{k}}}}}(p_iI_i + \overline{p_k}I_i);\tag {10}

$\begin{matrix} (11) & a_{k} (\bar{I_{k}^{2}} - {\bar{I_{k}}}^{2} + ε) ＝ \bar{p_{k} I_{k}} - \bar{p_{k}} \bar{I_{k}}; \end{matrix}$ a_k(\overline{I^2_k} - \overline{I_k}^2 +\varepsilon)　＝　\overline{p_kI_k} - \overline{p_k}\overline{I_k};\tag {11}

最终，ak等于：

$\begin{matrix} (12) & a_{k} ＝ \frac{(\bar{p_{k} I_{k}} - \bar{p_{k}} \bar{I_{k}})}{(\bar{I_{k}^{2}} - {\bar{I_{k}}}^{2} + ε)}; \end{matrix}$ a_k　＝　\frac{(\overline{p_kI_k} - \overline{p_k}\overline{I_k})}{ (\overline{I^2_k} - \overline{I_k}^2 +\varepsilon)};\tag {12}

另外， μk和 $σ_{k}^{2}$ σ^2_k 分别是引导图在ωk窗口中的均值和方差，最终ak和bk为：

$\begin{matrix} (13) & a_{k} = \frac{\frac{1}{| ω |} \sum_{i \in ω_{k}} I_{i} p_{i} - μ_{k} {\bar{p}}_{k}}{δ_{k}^{2} + ϵ} ； \end{matrix}$ a_{k}=\frac{\frac{1}{\vert\omega\vert}\sum_{i\in\omega_{k}}I_{i}p_{i}-\mu_{k}\overline{p}_{k}}{\delta_{k}^{2}+\epsilon}；\tag {13}

$\begin{matrix} (13) & b_{k} = \bar{p_{k}} + a_{k} μ_{k}; \end{matrix}$ b_k = \overline{p_k} + a_k\mu _k ;\tag {13}

将公式（13）带入公式（1），可以发现像素qi是由 k x k 个ak和bk计算出来，如下图所示。

为了简单起见，作者直接对在像素为i点位置的ak和bk做平均，即

${\bar{a}}_{i} = \frac{1}{| ω |} \sum_{k \in ω_{i}} a_{k}$ \overline{a}_i = {\frac{1}{\vert\omega\vert}\sum_{k\in\omega_{i}}a_{k}}

${\bar{b}}_{i} = \frac{1}{| ω |} \sum_{k \in ω_{i}} b_{k}$ \overline{b}_i = {\frac{1}{\vert\omega\vert}\sum_{k\in\omega_{i}}b_{k}}

最终，式（1）为

$\begin{matrix} (14) & q_{i} = {\bar{a}}_{i} I_{i} + {\bar{b}}_{i}; \end{matrix}$ q_{i}=\overline{a}_iI_{i}+\overline{b}_i;\tag {14}

3.3 代码讲解

由式（12）可以得知，要计算ak得计算：

1） $\bar{p_{k} I_{k}}$ \overline{p_kI_k} ：输入图*引导图，然后求均值；

2） $\bar{p_{k}} \bar{I_{k}}$ \overline{p_k}\overline{I_k} ：输入图与引导图的均值相乘；

3） $σ_{k}^{2}$ σ^2_k ：输入的方差，即输入平方的均值减去输入均值的平方；

4）对ak求均值，得到ai；

要计算bk得计算:

1）只需要输入图和引导图的均值，以及ak就可以了；

2）对bk求均值，得到bi；

最终的物理意义：

如果方差较小，即是一个平滑区域的话，那么方差较小约等于0，则ak约等于方差除以ϵ，因此 ak 约等于 0 。那么bk约等于1, 那么qi = mean(p)，这样相当于说这个pixel在该窗口内的输出值相当于在这个窗口进行了均值平滑，而考虑到pixel属于多个窗口，如果这是一个平滑区域，那么就相当与多个均值平滑滤波器的级联。
如果方差大，即是边缘的话，ak 就约等于 1 ，因此，b 就约等于0。相当于输出等于输入只是乘以一个约等于1的系数，这样可以保证梯度的比例关系不变。

C++code 如下：

cv::Mat GuidedFilter(cv::Mat& I, cv::Mat& p, int r, double eps){
  int wsize = 2 * r + 1;
  //数据类型转换
  I.convertTo(I, CV_32F);
  p.convertTo(p, CV_32F);

  //引导图的均值
  cv::Mat mean_I;
  cv::boxFilter(I, mean_I, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);/

  //输入图的均值
  cv::Mat mean_p;
  cv::boxFilter(p, mean_p, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);

  //输入平方的均值
  cv::Mat mean_II;
  mean_II = I.mul(I);
  cv::boxFilter(mean_II, mean_II, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);//盒子滤波

  //输入图*引导图，然后求均值
  cv::Mat mean_Ip;
  mean_Ip = I.mul(p);
  cv::boxFilter(mean_Ip, mean_Ip, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);//盒子滤波

  //方差
  cv::Mat var_I, mean_mul_I;
  mean_mul_I=mean_I.mul(mean_I);
  cv::subtract(mean_II, mean_mul_I, var_I);

  //步骤2
  cv::Mat cov_Ip;
  cv::subtract(mean_Ip, mean_I.mul(mean_p), cov_Ip);

  //a=conIp./(varI+eps)
  //b=meanp-a.*meanI
  cv::Mat a, b;
  cv::divide(cov_Ip, (var_I+eps),a);
  cv::subtract(mean_p, a.mul(mean_I), b);

  //meana=fmean(a)
  //meanb=fmean(b)
  cv::Mat mean_a, mean_b;
  cv::boxFilter(a, mean_a, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);
  cv::boxFilter(b, mean_b, -1, cv::Size(wsize, wsize), cv::Point(-1, -1), true, cv::BORDER_REFLECT);

  //q=meana.*I+meanb
  cv::Mat q;
  q = mean_a.mul(I) + mean_b;

  //数据类型转换
  q.convertTo(q, CV_8U);

  return q;
}

4. 总结

guided filter已经集成到opencv-contrib里面了，但其实这个版本的性能并不快，后续code推出来快速版本fast guided filter，原理是下采样后求ai和bi，正常分辨率下算法性能能到10ms左右。当然，如果你会SSE优化的话，优化这个版本会快到1 - 2ms。

guided filter其实是有些缺点的，因为它本质上还是一个局部窗口均值算法，这种算法就会在边缘的地方出现artifact，另外ϵ是一个定死的常数，这其实不利于全图约束。所以后续的方法中，也有将guided filter用于网络学习，来学习这个ϵ可能是一种更好的方式。

guided filter其实不仅仅只是保边平滑，因为它可以输入可变的guided image，如果你从事图像处理行业的话理解引导滤波会在后续解决问题的时候对你帮助很大。

我最近也在探索保边上采样的传统算法，而这个系列就是为了这个任务开的坑，希望这个坑能填完。

最后有什么问题可以在评论区交流。

ref:

[1] https://www.researchgate.net/profile/Xiaoou-Tang/publication/236228168_Guided_Image_Filtering/links/54e999640cf27a6de1103c64/Guided-Image-Filtering.pdf;

[2] https://zhuanlan.zhihu.com/p/161666126;

[3] https://blog.csdn.net/weixin_43194305/article/details/88959183

编辑于 2023-02-25 20:12・IP 属地四川

滤波算法

Guided Filtering的开端

一. 前言

二. 背景

三. guided filter方法

3.1 提出guided filter的原因

3.2 guided filter

3.2.1 介绍

3.2.2 引导滤波的能量函数

3.3 代码讲解

4. 总结

文章被以下专栏收录

算法

推荐阅读

论文解读：Uncertainty-Guided Probabilistic Transformer

论文解读：End-to-End Object Detection with Transformers

论文解读：End-to-End Object Detection with Transformers

DERT End-to-End Object Detection with Transformers