从0开始建立相机传感器的噪音模型-理论篇
网上的相机评测,low-level领域的论文中描述了相机数字CMOS的噪音特性和各种'规律‘和形形色色的标定方法。比如本专栏的前几篇文章对噪音的描述是比较公认的,比如在图像的方差图图中,shot noise为线性分量,PRNU为二次函数。但是这些'常识' 虽然口口相传,但是关于数学或者数据的支持却很少。
本文的目的从0开始,用数学和统计学观点 ,用最简单的公式解释噪音的期望和方差的关系,不同来源的噪音和 光子传输曲线(Photon Transfer Curve):噪音和信号的关系。
目录
1 图像噪声
2 一个简单的相机sensor数学模型
2.1 shot noise
2.2 read noise
2.3 PRNU noise
3 公式总结
4 噪音参数估计实践
1 图像噪声
图像噪声是在图片每个通道(RGB,RGGB,RYYB,YUV。。。)像素中亮度的随机变化,像素的期望本应该是均匀的或者是变化平缓的(如Total Variation的去噪原理)。在黑暗区域,当图像被放大仔细检查时,它更容易被注意到。噪声可以描述为由“亮度噪声”和“颜色噪声”组成,其中“亮度噪声”是保持整体色调基本一致的噪声,“色度噪声”中也有色调的变化。然而,由于噪声是随机变化的,其存在的原始图像总是涉及到这两种类型的噪声。请看下面的例子:
除了生成图片,艺术需求外,颜色噪音几乎总是不受欢迎的。然而,亮度噪声有时却需要保留避免模糊或塑化外观(工业界的ISP tuning去噪强度不会过强),如下面2张图:
由于噪声是亮度变化,所以最好用标准差统计量来测量它。从现在起,当提到噪声量时,我们将讨论图像亮度变化的标准差(通常用希腊字母σ表示),标准偏差是方差的平方根,方差表示为σ²。
人类的视觉系统只能分辨亮度1%以上的变化:
人眼这种基于对比度来检测亮度变化的方法意味着,相同的噪声水平在平均光度较低时更明显,而在平均光度较高时则不太明显。这意味着,衡量噪声的视觉影响的最好方法是考虑噪声与包含噪声的图像区域的平均光度之间的比例。表示这个比例的“经典”方法是通过信噪比(通常缩写为S/N或SNR):平均亮度除以噪声(标准差)。由于平均亮度和标准差都在ADUs中给出(ADU:一种无量纲的度量单位,也就是RAW图像的值),因此信噪比是无量纲的。
由于信噪比可以有很宽的取值范围,通常用其对数来表示。这可以是一个以2为底的对数,在这种情况下,信噪比用SNR_Stops表示: SNR_Stops = Log₂(SNR) = Log₂(Mean/Noise)
也有人会用分贝来表示: SNR_dB = 20⋅Log₁₀(SNR) = 20⋅Log₁₀(Mean/Noise)
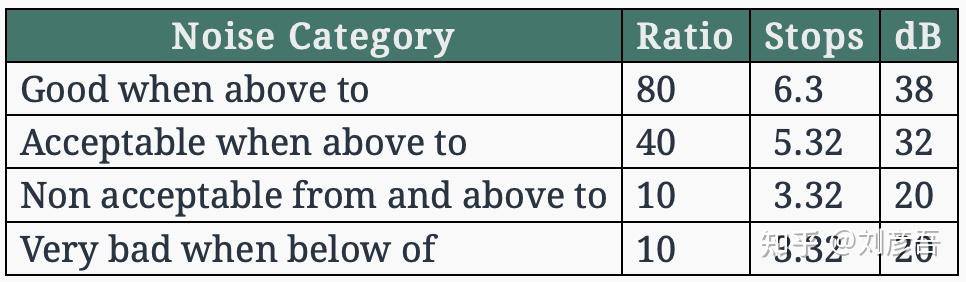
如在下表中,是一个DxO Mark相机评测的SNR结果,我们能看出几种SNR表示的关系:
我们在图像编辑中最好保证SNR不要下降,在线性模式中,我们直接提升图片亮度,SNR并不会改变,如果进行gamma校正这可能会降低SNR。SNR只是一个数字,一个计算结果,正如PSNR不一定准确衡量图片质量一样,SNR相同的噪音,其空间频率不同,人眼的感官差别很大,如下图:
根据环境条件(瞳孔大小),健康的人眼可以分辨50-100 cy/deg,如下图所示,该图显示了平均的人眼MTF(可参考下面的wikipedia),让我们回想一下,人类从1%开始分辨对比,这就是为什么“增益”从0.01开始。
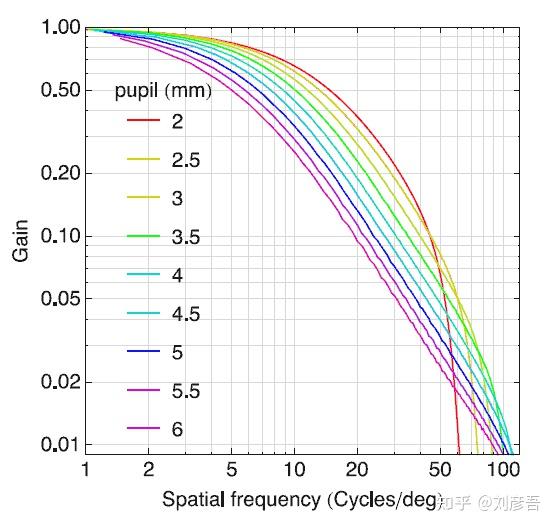
对于给定的观看距离,我们可以使用下面的公式得到cycle大小。一个cycle以两个图像像素(屏幕上)或点(打印时)为标准。
Cycle_Lenght = 2⋅Distance⋅Tan(Degrees_per_Cycle/2)
假设我们有一幅噪声为50信噪比的图像,我们发现该噪声的大小为1.7像素,这意味着cycle 为3.4pixel/cycle。如果我们以600 dpi打印该图像,每个cycle的长度为(25.4mm/inch)/(600pixel/inch)4pixels /cycle = 0.144 mm/cycle。在45cm的观察距离下,该cycle的空间频率为54.6cycle/degree(使用上述公式的反向计算)。如果我们观察人眼的平均MTF(例如,瞳孔径为4mm),我们会发现54.6个cylce/degree的增益约为0.04。这意味着对比度为1:50(50信噪比)的噪声将衰减到0.04:50(增益为0.04),“对应”的噪声为62分贝,观察者不会看到。
现在我们知道:图像分辨率(像素/mm)、观看距离、噪声大小、信噪比和观看环境(瞳孔大小)都会决定噪声对所观看图像的影响,更复杂的是人眼对不同单色光和白光的响应不同(白平衡)。ISO标准15739:2013"Photography - Electronic still-picture imaging - Noise measurements"规定了如何考虑到所有上述因素测量相机噪声。
本文主要研究了相机噪声的表示、组成及其数学关系。考虑噪声清晰可见的情况,如MTF gain为1。
2 一个简单的相机sensor数学模型
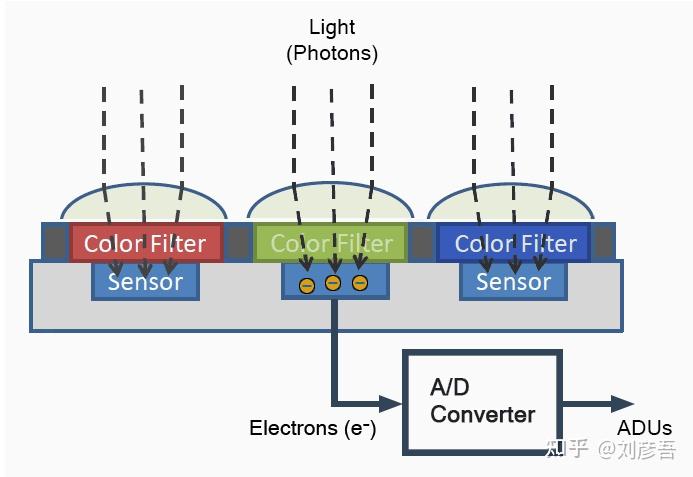
正如在之前的文章中提到的的,每个相机像素只对一种RGB(红、绿、蓝)颜色分量敏感,下图简单描述了DSLR相机传感器如何将击中它的光子转换成ADUs中的RGB像素值。
在曝光时照射到传感器上的光,可以用光子来描述。当每个光子到达传感器上的特定层时,光子就会产生一个电子。电子数量的单位是“e-”。一旦曝光时间结束,photosite电路中的ADC(模拟数字转换器)计算每个photosite中有多少电子,并将其转换为ADUs。在这种电子量化中,我们可以说,ADC使用转换因子“M”(来自乘法器),以“ADU/e-”为单位,乘以电子数,得到相应的ADU值。在曝光开始前,所有的photosites将重置。“M”大小仅取决于相机的ISO设置。当ISO值越高,“M”就会越高,制造相同ADU需要的电子就会越少,光敏越高。
击中每个photosite的光子通量与光的强度成比例。拍摄场景中较暗的区域将对应于较低的电子数,从而导致较低的ADU值,而较亮的区域将对应于较高的ADU值。我们将在曝光时间结束时,用符号“EL”(电子)和单位e-表示每个照片中的电子数。到目前为止,我们的传感器模型是:
2.1 Shot Noise
到目前为止,在我们的模型中,乍一看我们似乎还没有噪声的来源,其实我们已经有了,它是由“EL”表示的电子数。即使是在完全均匀的光照下,每个photosite的电子数也不一样。光子数是一个随机变量而不是一个常量;图像表面上的这些不同的值就是所谓的光子散粒噪声。为了理解这一点,让我们想象许多相同的杯子放在相同的雨下,雨结束时没有杯子溢出
如果在雨后,我们检查一下杯子,我们会发现每个杯子收集的雨水与其他杯子并没有太大的不同。但如果我们非常精确地测量,我们会发现每个杯子里的雨量是不同的。类似的情况也发生在光子撞击photosite的过程中。即使光子通量是常数,光子的数量,每个photosite生产的电子不是一个常数,而是一个随机变量遵循泊松分布。泊松过程被描述为“在固定的时间和/或空间内发生的离散事件的给定数量,这些事件以已知的平均速率发生,独立于自上一个事件以来的时间”。在我们的例子中,离散事件是光子产生电子的瞬间,“在一个固定的时间和空间”对应于每个感光点表面的曝光时间,其速率实际上与之前到达的任何光子无关。
当然,我们可以对之前的解释持怀疑态度。毕竟,我们讨论的是光以光子的形式到达并产生电子,我们需要更多的证据来接受这一点! 为了使“电子是沿泊松分布产生的”这一结论更加可信,我们做了一个小的“实验”。我们已经拍了34张照片,在相同的条件下,同一个图表,焦点有点模糊。下面是其中一张照片。
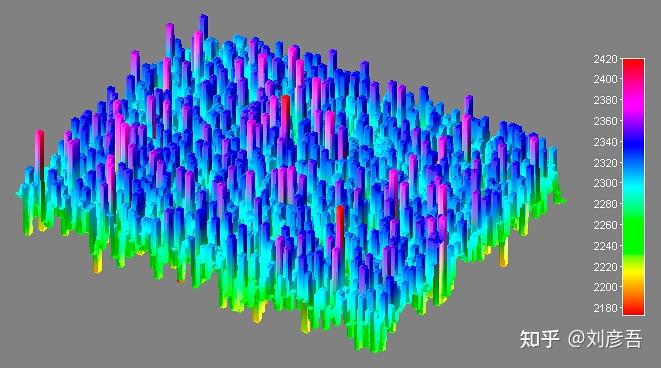
该图表包含35个不同亮度的“相机原始中性色”patch。从一个RAW照片文件中选择一个patch,我们分离了两个绿色raw通道中的一个,找到了光照最均匀的矩形区域(68 × 54像素:3672个“观测值”),并分析了它的分布。下图是3D中的样本像素值
任何均值高于1000的泊松分布都非常接近正态分布。因为我们的抽样值的平均值是2,287 adu,我们离那个参考标记相当远。这意味着我们可以认为我们的样本像素值来自一个正态分布。让我们用一些基于R的正态性测试来验证这一点。Shapiro–Wilk和Anderson-Darling normality test的p值都大于0.05,数据来自正态分布不能被广泛拒绝:
>shapiro.test(crop$Pixel_Value)
"Shapiro-Wilk normality test"
W = 0.9995, p-value = 0.3989
>library(nortest)
>ad.test(crop$Pixel_Value)
"Anderson-Darling normality test"
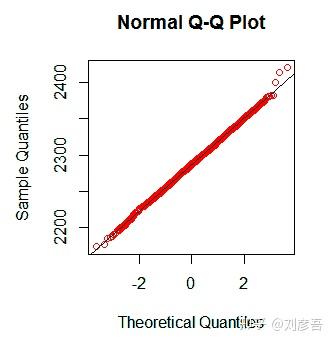
A = 0.4526, p-value = 0.2719另一种方法来比较样本概率分布叫做Q-Q plot,当两个分布是相似的Q-Q plot在y = x附近,样本与正态分布的Q-Q plot为:
我们发现数据符合均值较大的泊松分布,接近正态分布。虽然我们只是在一个镜头中使用了一个patch。尽管如此,有一种方法可以让我们更有说服力地测试光子shot噪声是否服从泊松分布:泊松分布有一个特殊的特性,即其均值等于其方差。
通常用希腊字母λ表示泊松分布的均值和方差,我们将在以下方程式中这样做:λ将表示每个照片点的电子数的期望值和方差。λ是无量纲的。尽管如此,为了使方程更容易理解,在表示期望值或噪声(标准差)时,它与虚构的单位ADU一起使用,在表示方差时,它与ADU²一起使用。
原模型原型方程两边的期望和方差:
现在,将上一个方程中的Mλ替换为期望公式,得到:
由公式2可知,在噪声具有泊松分布的假设下,图像亮度方差(噪声的平方)与其期望呈线性关系。
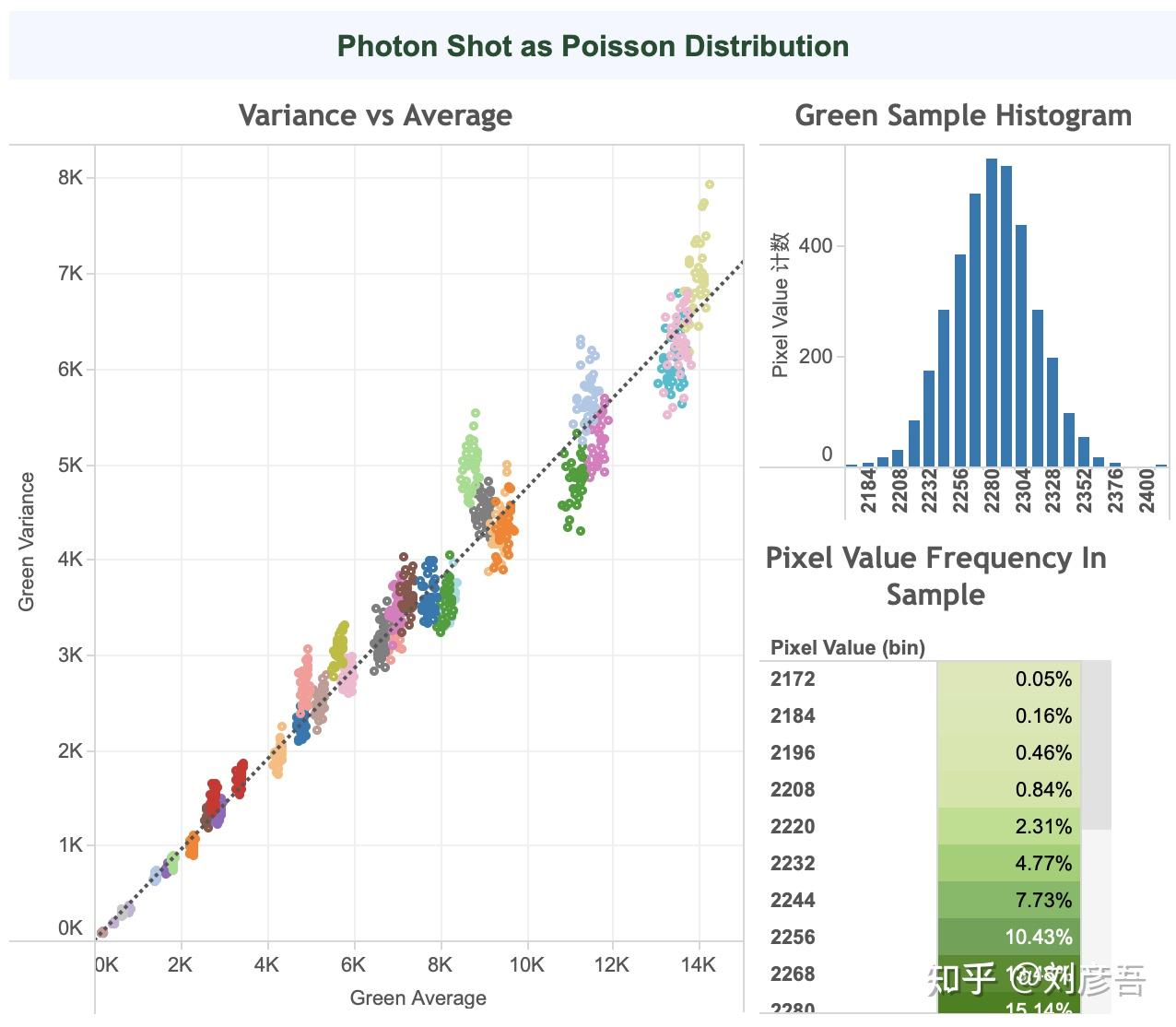
作为方差和期望的估计值,我们可以使用我们前面展示的图表的34个raw文件中的35个patch的样本平均值和方差。为此,我们从绿的raw图像像素中获取了每个补丁的正方形样本(每边60个像素),并计算了每个样本中3600个像素的方差和平均值。
在下面的图像中,我们展示了每个样本方差(纵轴)与平均值(横轴)的图表,其中来自图表中同一patch的数据具有相同的颜色。我们可以看到它们是如何形成线性关系的。图中所示虚线相关系数(R²) 为0.993 ,p值小于2.2e-16。这张图还显示了正态分布测试的样本的直方图,我们可以看到高斯钟形。
如果光子shot噪声是图像中唯一的噪声源,那么SNR将是收集到的电子数的平方根(λ的平方根在下面的方程中)。注意,这是光的物理特性所施加的信噪比极限。
最后一个方程表示了理想相机传感器的信噪比,其中唯一的噪声源是自然光,没有其他噪声源。当信噪比以对数方式表示时,光子shot噪声信噪比表示为一条斜率为½的直线。如果我们对上述方程的两端取对数,我们得到:
关于光子shot noise的总结:
- 它与平均亮度的平方根成正比。这意味着它方差随亮度(或信号)线性增长。
- 它服从泊松分布,ADU大于1000时近似为高斯分布。
- 其信噪比随光度的平方根而增大。
2.2 Read Noise
下面的方程是我们当前的sensor模型。“EL”项,代表photosite收集的电子数量,是一个随机变量,我们将用粗体。
在APS (from Active Pixel Sensor)传感器中,每个photosite连接一个电路,将光子撞击产生的电子的电荷转换为电压,并将其作为输入到A/D转换器。由于这条处理线不是完美的,ADC的输出并不完全与光子发射的电子数量成比例。镜头盖上拍摄的照片,从ADC出来的ADU总是有一个偏差或基线(为了保留暗区信号,在ADC之前会有一个黑电平)。这种噪声称为read noise。
下面的动画解释了读取噪声baseline是如何从ADU值中剪掉的,但read noise仍然停留在图像中。
- 传感器read noise。平均500 ADU的“假信号”(在这个例子中)。图中噪声的强度用翡翠色带表示。
- 从照片中收集的信号。即使光源以300 ADU的期望值均匀照明,信号(红色细线)也不是平坦的,因为它包含光子shot noise。
- ADC的输出,用红色粗线表示,包含read noise和信号。它比步骤(2)中的原始信号包含更多的噪声,因为它也包含read noise。
- read noise“校正”。从ADU值中减去read noise“假信号”。如果此减法的结果是负值,则像素设置为零。现在红色信号的平均adu达到了预期的300,但是来自读取噪声的附加噪声仍然存在:翡翠带的高度与步骤3相同。这一部分其实就是黑电平校正,有的相机会自动做,或者也可以后处理。
下面的动画从直方图角度显示了上面的相同步骤。
我们将使用“RNS”将read noise添加到我们的模型中,用粗体字是因为它是一个随机变量。
为了简化我们的公式,“RN”将表示read noise,“RN²”将表示其方差:
Var(RNS) = RN²
StdDev(RNS) = RN
上面的公式告诉我们,在有read noise的图像中,平均像素值是由信号和read noise加起来的。我们可以通过减去μRNS来修正RAW图像(可以理解为黑电平校正):
在上面第一个方程的左侧,下标为“RNC”的ADU项,代表“read noise校正”后的raw图像中的ADU值。在“read nosie校正”后,将read noise“假信号”从ADU值中减去其平均值。这样,正如我们在上面的第二个方程中看到的,“read nosie校正”后的RAW图像的期望值就不会有read noise“假信号”。注意RNS是一个随机变量,但是它的平均μRNS是一个常数。
注:这里的Read noise其实包含两部分,一部分是一个固定的baseline(黑电平),一部分为正态分布。此后讨论的ADU都是经过平均read noise校正的:
read noise完全独立于shot noise(有一部分文献认为他们在log域下成线性关系,可能对某些数据集的统计近似得到,但并无理论支持)。read noise与传感器电子器件的缺陷有关,与照射传感器的光的强度无关。相反,shot noise是由光的物理性质引起的,与光的强度有关,与传感器的处理完全无关。(注:read noise在黑帧中很明显,和增益的设置有关)read noise和shot之间的独立性意味着它们的和的方差等于它们的方差的和(正交)。
我们对上述方程的两端算方差。μRNS的方差为零:
现在我们可以得到当前模型的信噪比。记住,噪声是方差的平方根,也就是标准差。
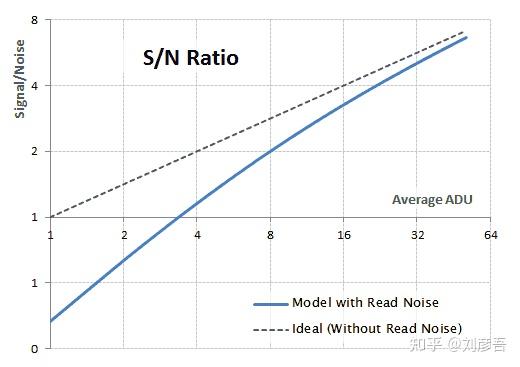
如果我们比较这个传感器模型(shot+read noise)和理想传感器(shot noise)的SNR,我们得到如下图所示的模拟:
上图说明read nosie在图像的较暗部分降低了信噪比。对于较高的亮度,read noise的影响逐渐消失,信噪比逐渐接近理想的信噪比传感器。read nosie对传感器的施加了一个下限,影响其动态范围。
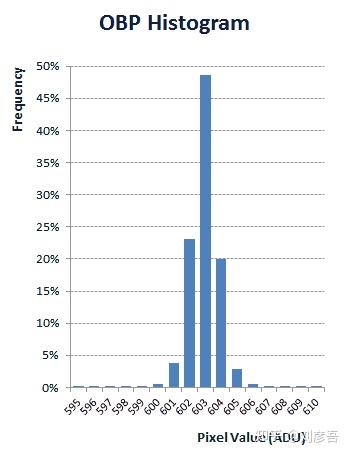
对于RAW的read noise去除,可以拍摄黑帧并减去黑帧平均,有的品牌会内置OB(Optical Black Correct),CMOS中的某些像素被覆盖用于自动校正read noise,如下图为OB的直方图:
可以看出,Read noise在相机中是一个有较大均值的高斯分布。
2.3 PRNU Noise
并不是所有的photosites都是一样的,对光线的敏感度也不是完全一样的。每个感光点上的微透镜(收集产生的电子的层)、A/D转换器和其他传感器电路元件在制造过程中并不是完全相同的。换句话说,在我们的模型中的“M”项,对于每个照片站点来说不是完全相同的值。相反,“M”是每个photosites的一个属性。这种情况称为像素响应不均匀性(PRNU)。
考虑到这一点,我们将因子“M”替换为“Mp”:我们将使用下标“p”来表示在每个给定的传感器位置“p”上,“M”随着每个photosites的变化而变化。
我们必须注意到,“Mp”的灵敏度变化并不是有意为之,它们是在不同像素点之间的随机变化。在这个意义上,Mp是一个关于传感器表面的随机变量。这个事实用上面公式的表示法表示——用粗体“Mp”表示。然而,我们将考虑到每一个像素,随着时间的推移,始终具有相同的“Mp”值。这意味着“Mp”,对于每一张照片,在保持相同的ISO速度(感光片的灵敏度随着ISO速度的变化而变化)的时间(在拍摄之间)是一个常数。
传感器表面所有光斑对应的所有“Mp”因子的平均值(统计上称为期望值)是一个常数。这个平均值可能就是制造过程的目标。我们将这个平均值称为“EM”(预期乘数):
我们将围绕这个平均值建立“Mp”模型。为此,我们将把“Mp”看作是由两个分量组成的(考虑到两个变量之和的Eva()的公式,这是合理的):一个是平均“EM”,另一个是相对于平均值的光敏性偏差。我们将后一个分量称为“MDp”(表示“M”的偏差):
注意,这种表达Mp的方式意味着MDp的平均值为零(Eva(MDp) = 0)。我们可以将期望值运算符应用到前一个方程的两端,并使用“Eva(EM) = EM”来探究这个问题:
根据上面对Mp的定义,将我们的传感器模型更新到公式9中,得到:
三个噪声源(用粗体字体表示)彼此独立。这将允许我们使用更简单的公式来得到期望值和所得ADU的方差。
ADU的空间平均值
对公式10两边求均值:
ADU的空间方差
两个独立变量的乘积的方差:
对两边取方差,划线的方差为0:
我们把MDp的方差称为PRNU²。请注意公式符号“PRNU”指的是photosites的标准差(ADU/e-),而不是PRNU在RAW图像中引起的噪声。
Var(MDp) == PRNU²
StdDev(MDp) == PRNU我们还利用下面几个前文提到的公式:
Var(EL) = λ
Eva(EL) = λ
Eva(MDp) = 0方差为:
这就是我们在本文一开始所寻找的等式。从传感器模型推导出一个简单的方程,从传感器的特性出发,解释了噪声的分布。注意方差是λ的二次多项式,它表示在photosites电子平均数。二次项是PRNU噪声和shot noise之间的协同作用。除了二次项,PRNU在线性λ项中也有影响,所有这些都告诉我们,PRNU可以是一个非常强的噪声源。噪声(标准差)就是上述公式12中方差的平方根。这样,信噪比为:
PRNU信噪比极限
如果PRNU是传感器中唯一的噪声源,那么总ADU方差主要是上述方差的二次项。在这种情况下,信噪比为:
信噪比是独立于电子数的。当我们考虑公式13中所有三种噪声类型时,这也是信噪比的上限。如果公式13中的λ值持续增长,得到的信噪比将始终低于我们在上面发现的SNR_PRNU值。幸运的是,对于大多数单反相机传感器来说,注意,信噪比是独立于电子计数的。当我们考虑公式13中所有三种噪声类型时,这也是信噪比的上限。如果公式13中的λ值持续增长,得到的信噪比将始终低于我们在上面发现的SNR_PRNU值。幸运的是,对于大多数单反相机传感器来说,由于λ很难接近上限(例如14位原始文件的16383 ADU),PRNU并且不会对SNR造成太大的损害。
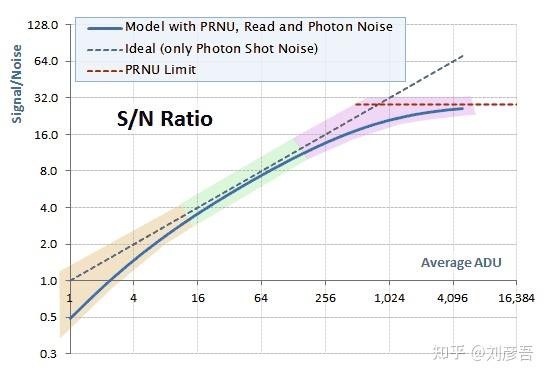
SNR中的三个噪声相位
在下图中,我们有一个模拟的信噪比曲线,我们可以区分出三个相位,显示我们所研究的每种噪声类型的优势。在曲线的左端,ADU值较低,在橙色背景区域read噪声使信噪比低于代表理想传感器的灰色虚线,只有shot noise。在第二部分,用绿色的背景显示,信噪比是由shot noise主导的,并“保持”在0.5左右的斜率。在右端,即粉色背景区域,信噪比减缓增长速度并开始弯曲,逐渐低于PRNU极限(见公式14),用红线虚线表示。
分离PRNU噪音
我们可以通过平均一组均匀光照表面的相同镜头(略微失焦)和过度曝光设置来隔离图像PRNU噪声,但要注意不要截断RAW图像(会改变噪音分布)。这样,我们将使PRNU噪声在图像上的存在感更强。注意,这个平均值指相同位置的像素在一组照片上的平均。
图像平均将突出PRNU噪声,因为对于一个给定的像素PRNU不会在不同照片中改变。然而,其他类型的随机 噪声(shot and read noise),平均后会减少。我们可以从下列公式中更清楚地看出这一点:
在这些公式中,当我们在一组RAW图像中平均相同的像素时,对每个固定的“p”下标进行求和。这就是为什么我们可以把MDp从第一个方程的和中提出来。平均图像数用“n”表示。对上一个方程的两端求方差,得到:
化简后:
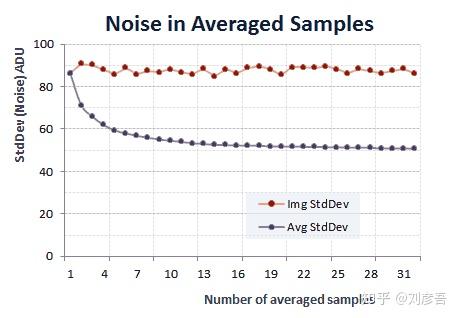
在上面的方程中,我们可以看到PRNU二次项是不受平均影响的,而其他种类的噪声的影响随着平均图像数量的“n”值的增大而减小。我们用相机镜头在iPad屏幕上拍摄了32张单色照片。生成的RAW图像的绿色像素值为其上限的87%。换句话说,他们过曝但并没有超出上限。为了显示平均对结果图像的方差的影响,下面的图表显示了每个单独图像的绿通道的噪声(标准差),以及由不同数量的照片的平均值产生的图像噪声。我们使用Iris软件(add_mean命令)获得了这些平均图像。
每一张照片都包含来自镜头渐晕额外的变化,出于这个原因,上面的图表显示了来自一个46 × 66像素的样本区域的数据。平均图像的噪声从大约20个样本下降到非常轻微。然而,我们求出了它们的平均值,得到了下图。色调曲线的应用使更容易看到镜头的渐晕。
如果我们从图像的中心到它的一个角落画一条线,并沿着这条线绘制像素值,我们会得到如下图所示的曲线,其中像素值的高频(空间)变化主要是由PRNU噪声引起的。虚光晕是导致总体趋势曲线呈弧形的原因。为了将PRNU噪声从镜头渐晕中分离出来,我们去掉了那个弧形,让PRNU噪声“越过”一条平坦的线。
消除镜头渐晕的一种方法是使用一种叫做Flat-Field correction的技术。在一般情况下,Flat-Field correction需要减去一个“暗帧”,以消除read noise和可能的其他类型的传感器噪声(如热噪声)。然而,对于尼康相机RAW图像文件中已经对读取噪声进行了校正,我们既没有曝光引起的热噪声,也没有在本文中考虑到它。
首先,我们将对平均图像去噪,应用一些Photoshop滤镜(强降噪和一些高斯模糊)来去除高频变化,只得到带有镜头渐晕的背景,我们将生成的图像称为“flat field”。
flat field的修正,我们在平均图像每个像素值除以相应的一个传感器(相同的位置坐标)的flat field图像,然后将结果乘以平场的像素值中值。
pixel(prnu_only, x, y) = [pixel(averaged_image, x, y)/pixel(flat_field, x, y)] * median(flat_field)
Where pixel(img, x, y) is a function allowing to get or set the value
of the pixel with coordinates (x,y) in the image file "img".
得到的孤立图像PRNU噪声如下图所示。这幅图像经过处理,使其结构更加明显。上半部分显示的是100%尺度的图像PRNU噪声;左下角有一块(清洁不当的)污迹。下半部分显示了图像的另一部分PRNU噪声,但在50%的比例,它使垂直图案更明显,但也有一些水平图案。
我们可以看到,PRNU噪声在空间维度上不是完全随机的,它可能可以分解为三部分:列、行和剩余的随机空间分量。抛开我们刚才所说的,对PRNU噪声样本的分析表明,它的分布非常接近正态分布:
> shapiro.test(prnu$PixelValue)
"Shapiro-Wilk normality test"
W = 0.9993, p-value = 0.03502
> ad.test(prnu$PixelValue)
"Anderson-Darling normality test"
A = 0.5389, p-value = 0.167
去除(大部分)PRNU图像噪声
消除大部分PRNU图像噪声的一种方法是逐像素地获取两张相同图像的差异:我们用相同的场景、光照和相机设置拍摄两张相同的照片:就像连续拍摄的两个静止目标的图像。请注意,在我们的命名法中,术语PRNU是像素灵敏度的标准差,这反过来会在图像中引起称为PRNU图像噪声的噪声。
我们的想法是,PRNU是由MDp引起的,它在相同的镜头之间保持不变,我们将能够删除它在这两个图像的差异。让我们通过模型中的方程来了解这个想法。我们将使用delta“δ”算子来表示在两个相同的镜头中来自同一像素的值的差值。(μRNS)作为恒定值是零。
由于“MDp”是一个photosite特性,并且在拍摄之间不改变,我们可以从delta算子中分解出这个术语。现在我们对最后一个方程的两边求方差。最终我们会得到如下结果:
注意上面等式的右边类似于ADUp方差公式12,但是它不包括PRNU方差的二次项。即使它包含了PRNU线性项(在λ中),PRNU方差(PRNU²)通常也比“EM²”项小得多。作为一个实际的结果,我们可以忽略PRNU²项,考虑结果只包含read 和 shot noise。
公式19告诉我们,如果我们计算两个相同的镜头之间的图像差异,并将其除以根号2,结果图像将包含只有shot nosie 和read noise。
下面的图像显示了一个例子(差分图像除以2的平方根)。
进一步的分析将显示read noise是相对很小的,上面的图像几乎只包含shot noise,正如预期-不包含任何pattern,几乎是高斯噪声。
Sensor噪声建模的公式总结
ADU:
其中“EM”是传感器将每个感光点的电子计数转换为像素值单位(ADU)的平均比率。“MDp”项表示在介质值“EM”附近的光斑灵敏度偏差,这两个项的总和是光斑电子计数到ADU单位的转换比率。photosite中的电子数用“EL”表示。“EM”和“MDp”以“ADU/e-”为单位,而“EL”以“e-”(电子)为单位。这样产品的结果就是“ADUs”。“RNS”是由传感器电路加到“真实信号”上的读噪声“假信号”偏置,用ADU单元给出。μRNS (ADUs中也有μRNS)是读取噪声“假信号”偏压的平均值,从photosite读取中减去该偏压以去除它。
我们必须区分阅读噪声的两种不同影响:(i)它增加了photosite值的偏置,也(ii)增加了它们的方差。读取噪声校正消除了偏误在photosite值,但即使如此,增加的方差留在图像中。
ADU的期望
ADU的方差
两张图片差的方差




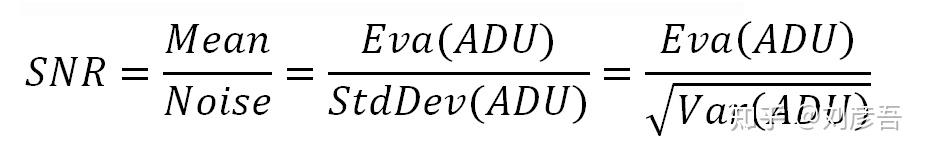
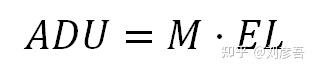


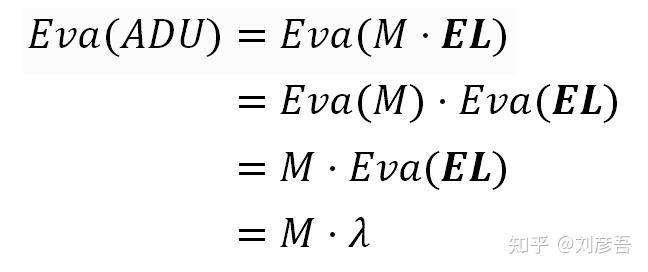
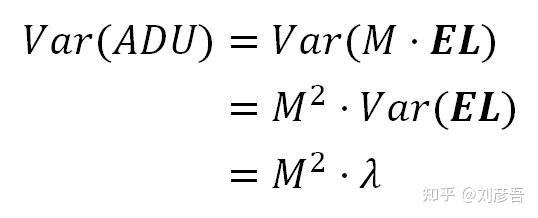
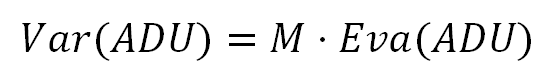
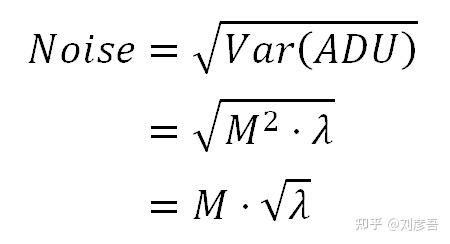
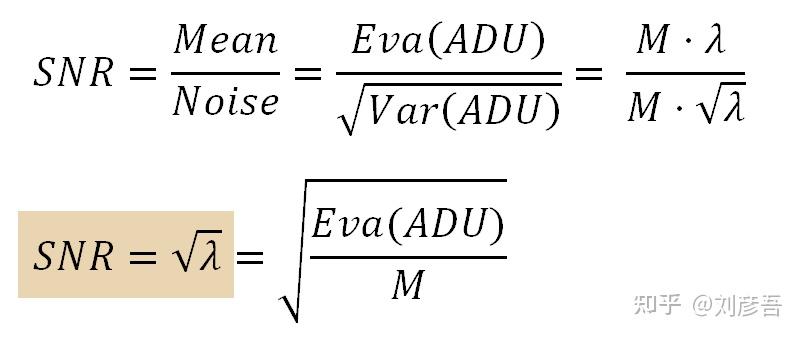

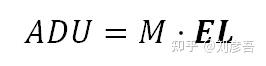
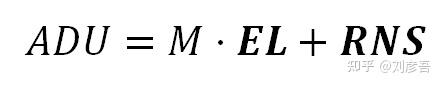
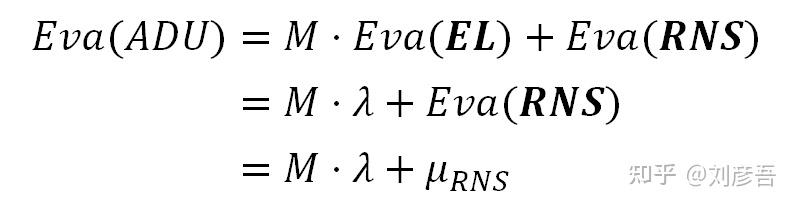
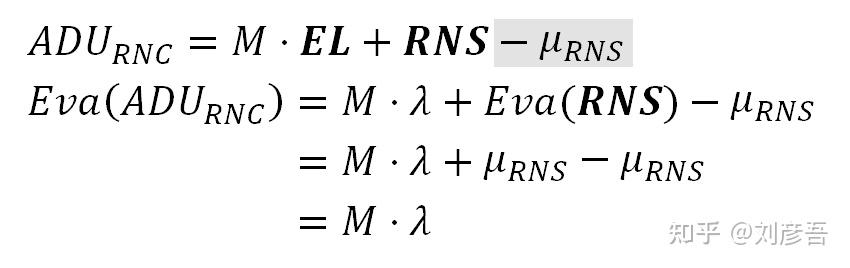
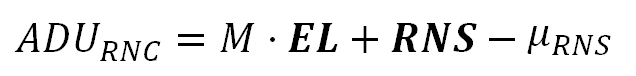
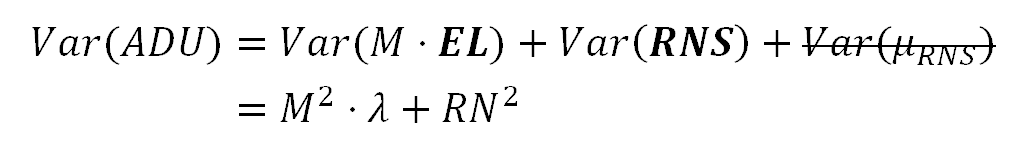
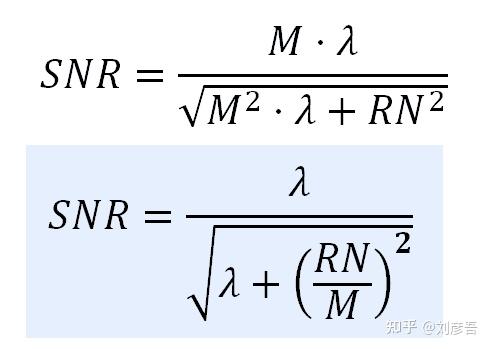
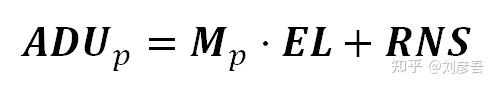
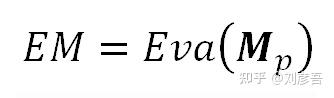
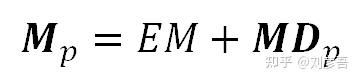
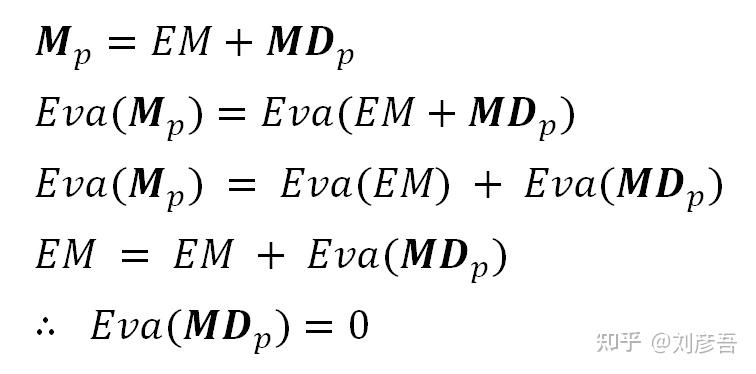
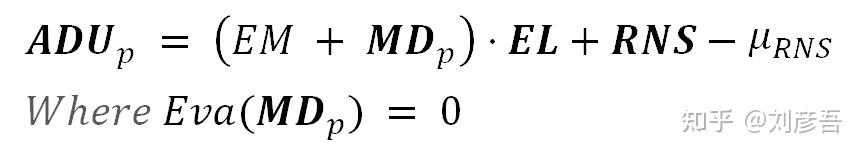
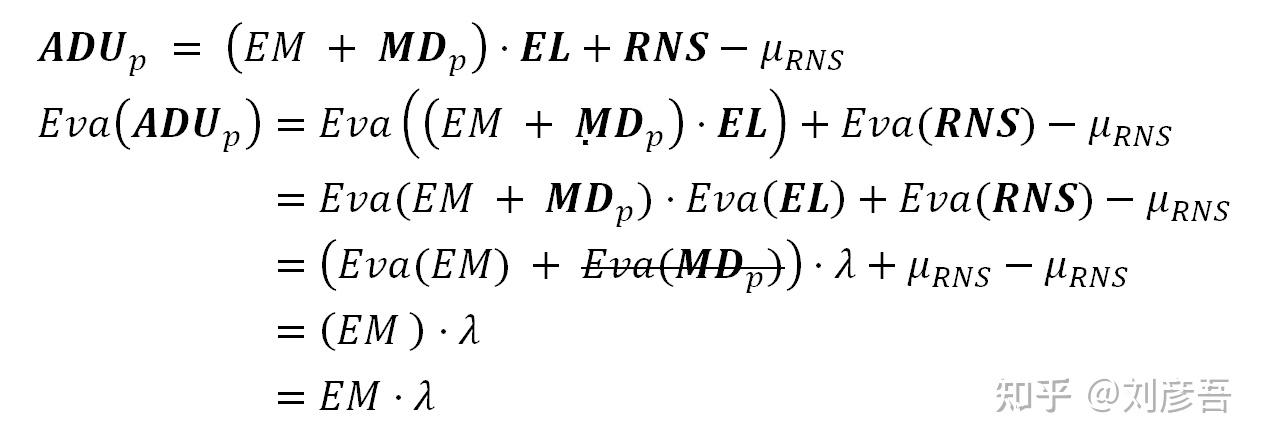
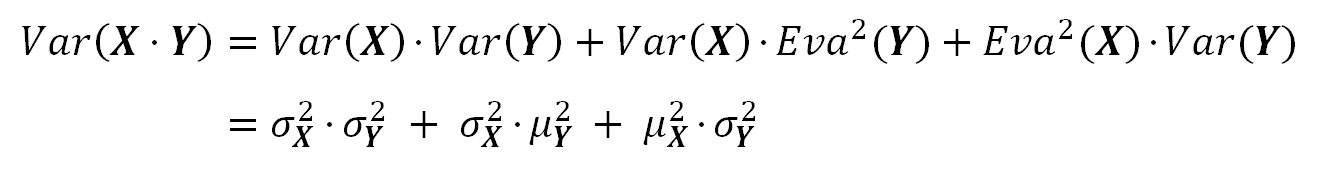
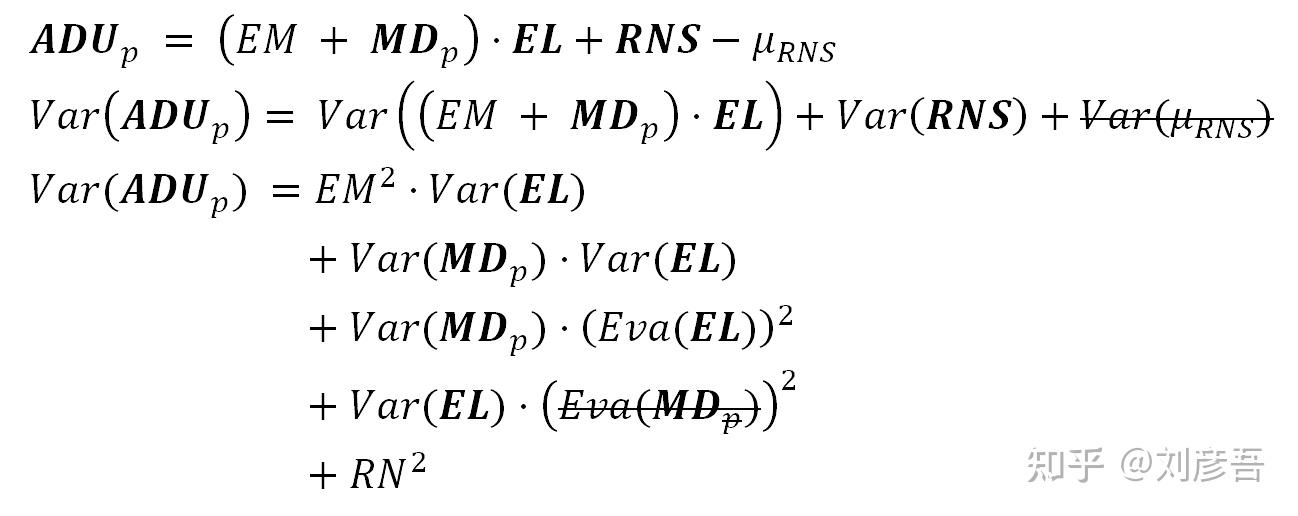
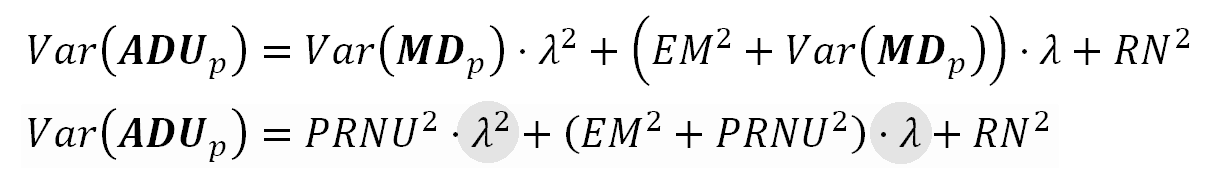
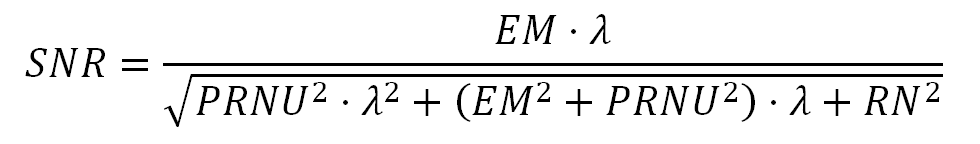
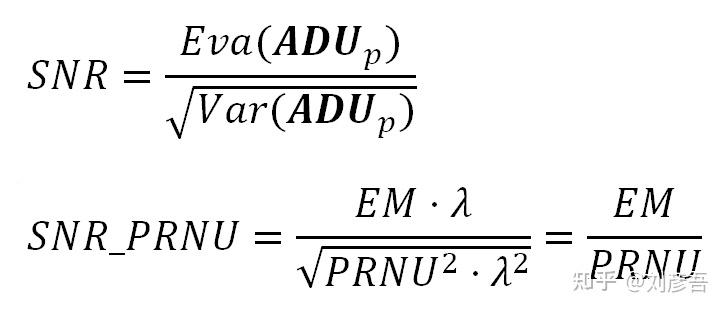

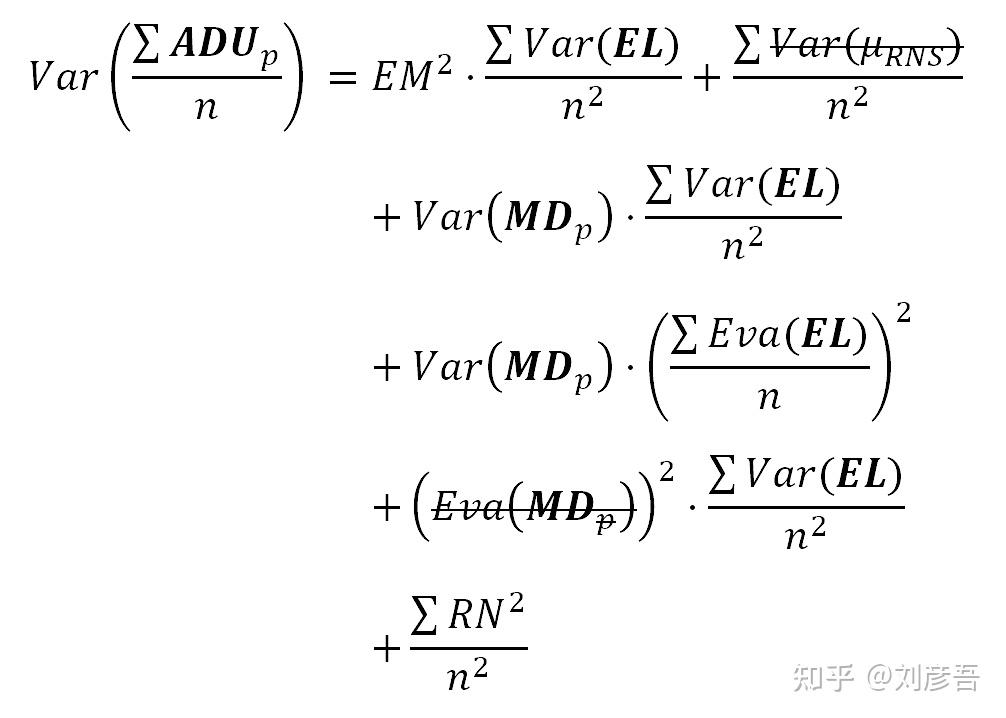
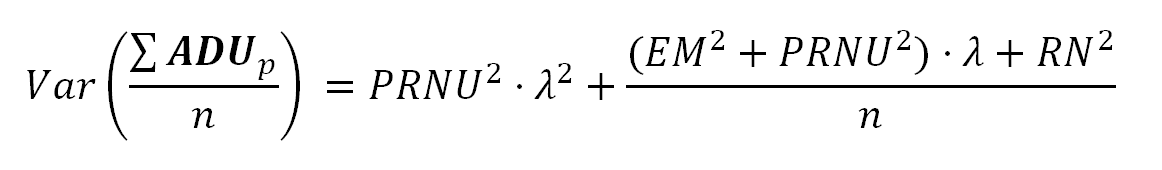


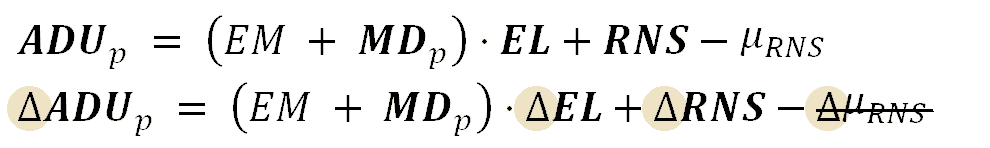
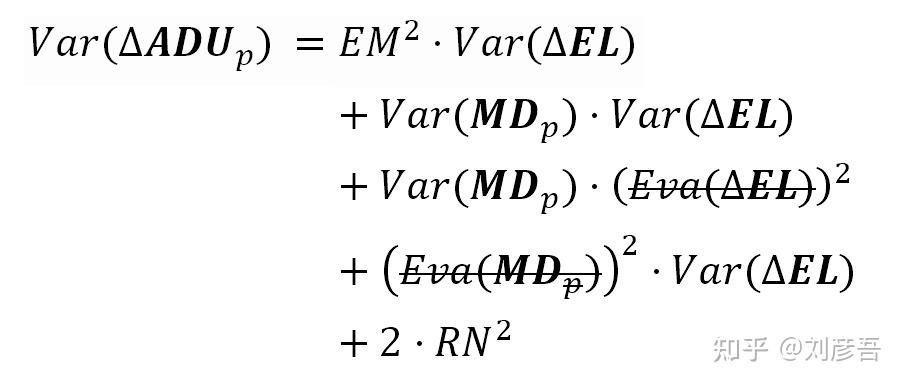
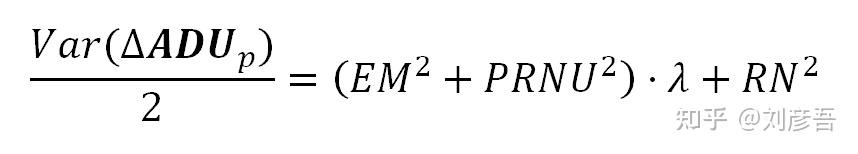

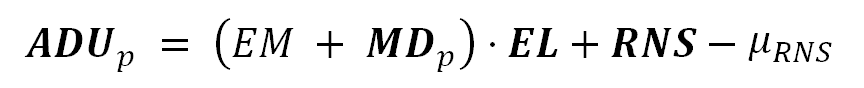
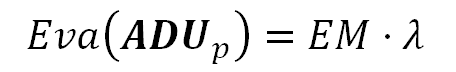
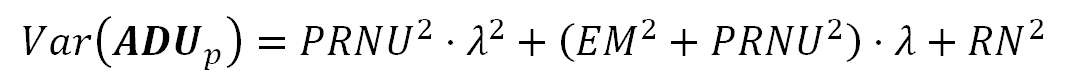
电路噪声的话可能很难根据Raw图去标定,其实实际操作中减去黑帧或者两帧相减对暗电流,PRNU,FPN也有一定的抑制效果,感觉现在大家还是更关注单个像素的统计规律吧,毕竟从高斯白噪时代到现在也没几年。。