图解卡尔曼滤波器,无需深厚的数学知识也易懂(第三部分:α−β−γ滤波器)
案例1: 称金子重量
现在我们已经有足够的基础看第一个简单的例子。在这个例子中,我们将估计静态系统的状态。静态系统是一个在合理时间内不会改变其状态的系统。例如,静态系统可以是一个塔,状态是它的高度。
在这个案例中,我们要估计金条的重量。我们有一个无偏差量度,也就是说,这个量度没有系统误差,但是在测量中依然会包含随机噪声。(误差分为内部外差/系统误差,外部误差/非系统误差,这就想说明的是非内部/系统误差)
在这个例子中,系统是金条,系统的状态是金条的重量。因为我们假设重量在短时间内不会改变,因此系统的动态模型是恒定的。
为了估计系统的状态(即金条重量),我们可以进行多次测量并取其平均值。
在时间n时, \hat{x}_{n,n} 的估计值是所有先前测量的平均值:
本例中的动态模型是恒定的,因此 \hat{x}_{n,n}=\hat{x}_{n,n+1} 。
注意:在文献中,变量上方有符号,如 \tilde{x} 表明就是估计值。
为了估计 \hat{x}_{N,N} 我们需要记住所有的历史测量值。假设我们没有笔和纸来记录测量值,我们也不能依靠记忆来记忆所有的历史测量值。我们只想使用之前的估计值并添加一个小的调整(在现实应用程序中,我们希望节省计算机内存)。我们可以用一个小的数学技巧来做到这一点:
\hat{x}_{n,n-1} 表示在时间N时x的预测状态,而这个预测状态时基于在时间N-1时的测量。换句话说, x_{n,n-1} 是上一次(相较于当前的上一次)的估计值。
上述方程是五个卡尔曼滤波器方程之一。它被称为状态更新方程State Update Equation(敲黑板:后面会一直用到这个方程,请大家务必熟练于心)。其含义如下:
系数 \frac{1}{N} 对于我们的示例是特定的。稍后我们将讨论这个系数的重要作用,不过现在我先指出,在卡尔曼滤波器中,这个因素被称为卡尔曼增益(Kalman Gain)。用 K_{n} 表示。下标n表示卡尔曼增益随每次迭代而变化。
K_{n} 的发现是Rudolf Kalman的主要贡献之一。
同时,在我们深入探讨卡尔曼滤波器之前,我们将使用希腊字母 \alpha_{n} 来表示这个系数而不是 K_{n} 。
因此,状态更新方程如下:
y_{n}-\hat{x}_{n,n-1} 是测量误差,也被称为innovation。innovation中也包含新信息。(注意, y_{n} 是系统在n时的测量值, \hat{x}_{n,n-1} 是对系统在n时的估计值)
在我们的案例中, \frac{1}{N} 随着N增加而减小。这意味着在开始时,我们没有足够的重量值信息,因此我们将估计值建立在测量的基础上。随着我们继续测量,由于 \frac{1}{N} 的减小,在估计过程中的每个连续测量的变化起的作用越来越小。直到某个点,新测量的贡献将变得微不足道。
让我们继续看这个例子。在进行第一次测量之前,我们可以通过读取金条上的图章来猜测(或粗略估计)金条的重量。这被称为初步猜测Initial Guess,这将是我们的第一次估计。
正如我们稍后将看到的,卡尔曼滤波器需要初始猜测作为预设,这个猜测可能非常粗略。
1.1 估计算法
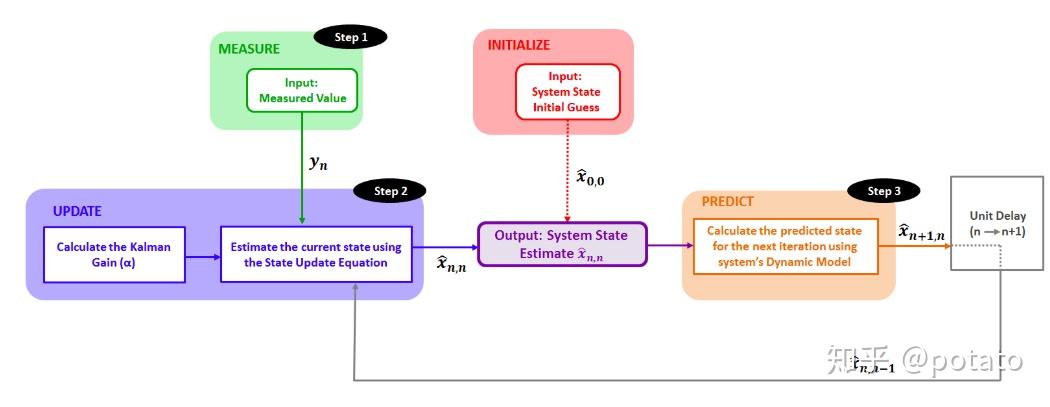
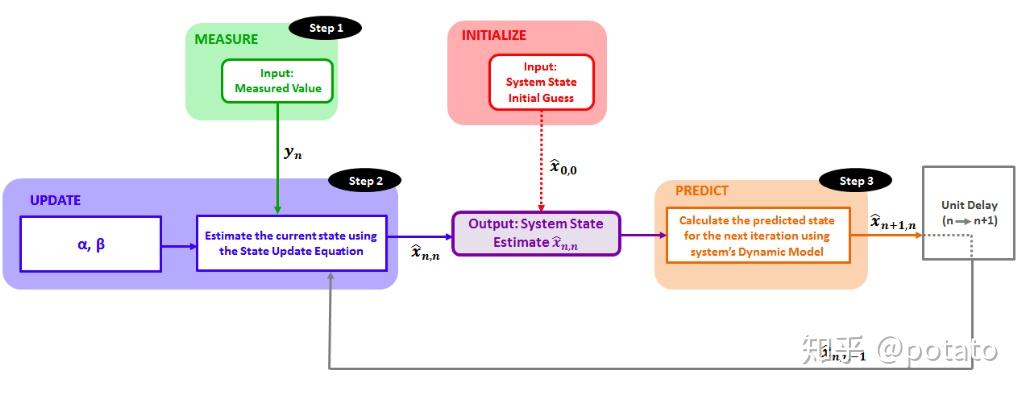
下图描述了本例中使用的估计算法。
现在我们准备开始测量和估计过程。
1.2 数值案例
1.2.1 第0次迭代
1)初始化
我们对金条重量的初步估计是1000g。滤波器初始化操作仅需一次,因此在下一次迭代中不需要它。
2)预测
金条的重量不会改变。因此,系统的动态模型是静态的。我们的下一个状态估计(预测)等于初始化:
1.2.2 第一次迭代
- step 1
用天平测量重量得到:
- step2
1)计算卡尔曼增益。在我们的例子中 \alpha_{n}=\frac{1}{n} ,因此:
2)使用状态更新方程计算当前估计值:
注意:在这个特定的例子中,最初的猜测可以是任何数字。由于 \alpha_{1}=1 ,初始猜测在第一次迭代中被消除。
- step3
系统的动态模型是静态的,所以金条的重量不应该改变。下一个状态估计(预测)等于当前状态估计:
1.2.3 第二次迭代
单位时间延迟后,上一次迭代的预测值predicted estimate将成为当前迭代的前一个估计值previous estimate:
- step 1
对重量进行第二次测量得到:
- step 2
1)计算卡尔曼收益Kalman gain:
2)计算当前估计值:
step 3
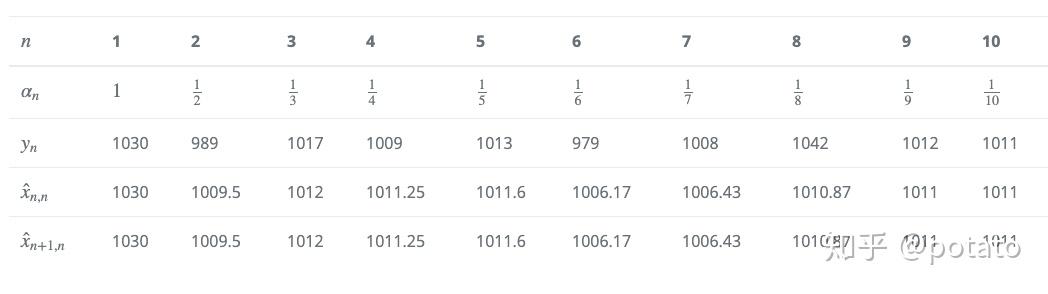
下面是第3至第10次迭代:
滤波器迭代现在可以停止了。每次测量卡尔曼增益都会减小。因此,每次连续测量的贡献都低于先前测量的贡献。我们的重量接近于1010克。如果我们进行更多的测量,我们会更接近真实值。
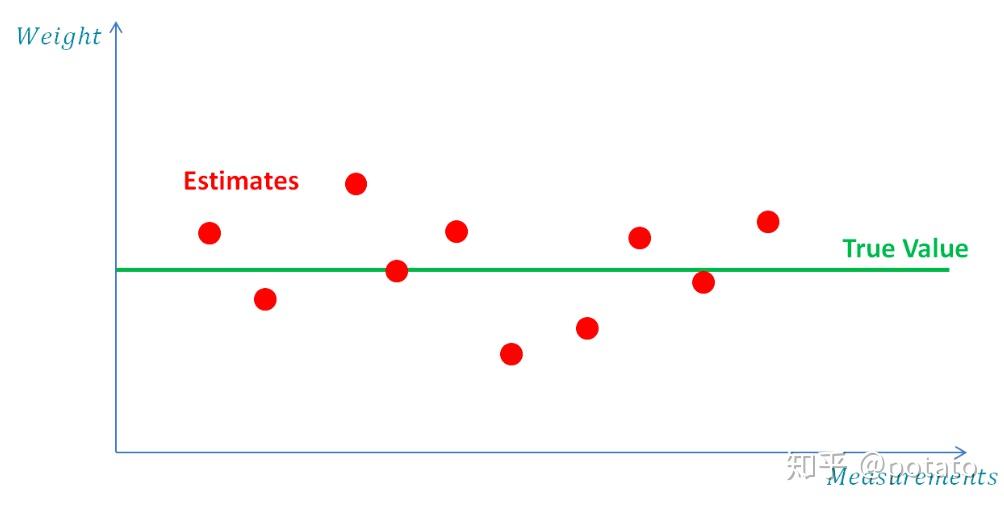
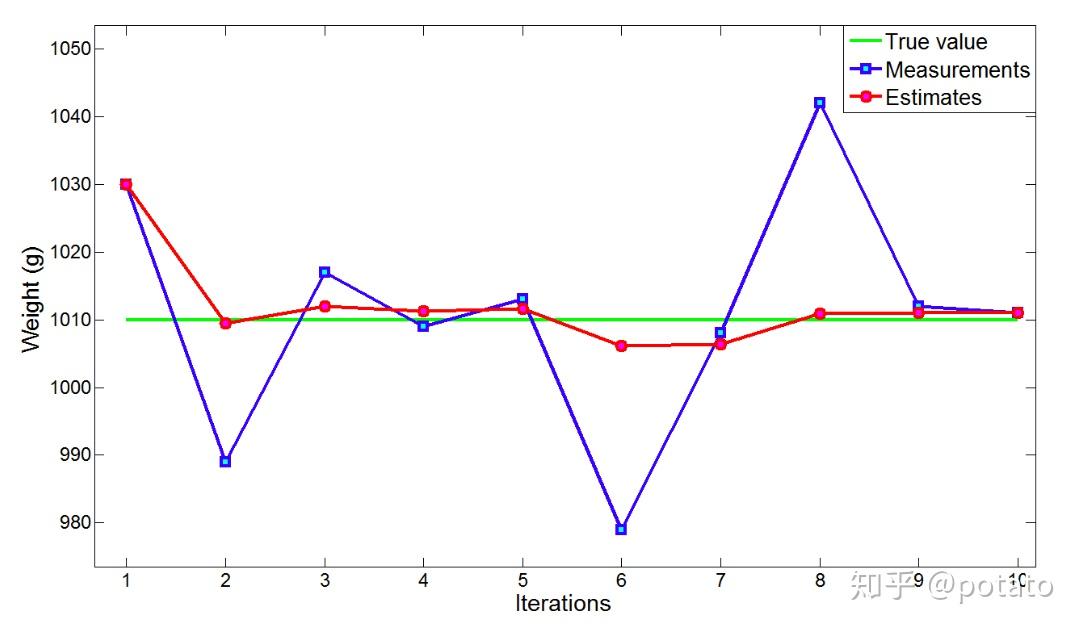
下表总结了我们的测量和估计,图表比较了测量值、估计值和真实值。
我们可以看到,我们的估计算法对测量有平滑的影响(意思是,估计算法会使得测量值变化减小),并且它收敛到真实值。
1.2.4案例总结
在这个例子中,我们为一个静态系统开发了一个简单的估计算法。我们还推导出了状态更新方程,这是五个卡尔曼滤波方程之一。
案例2 :跟踪一维匀速飞行器
现在做一个随时间改变状态的动态系统。在这个例子中,我们将使用α-β filter在一维上跟踪等速飞行器。
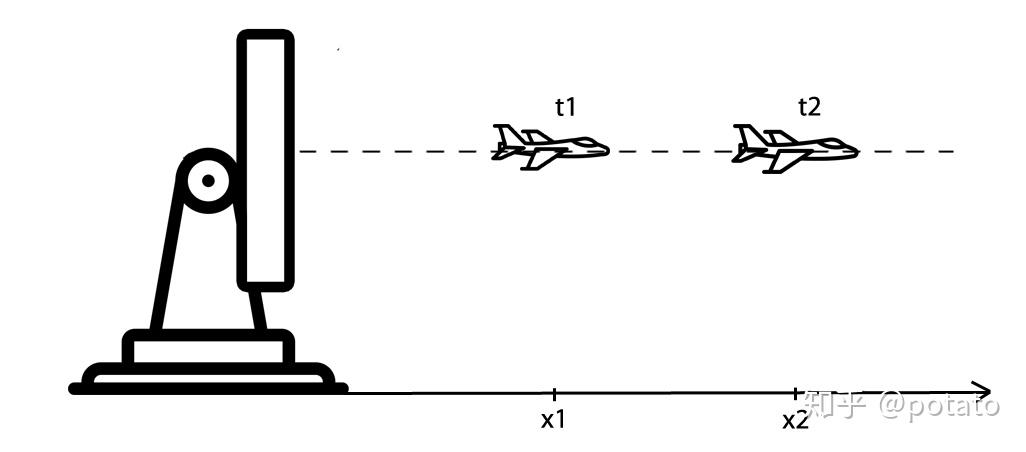
让我们假设一个一维的世界。我们假设一架飞机正在朝向远离雷达(或朝向雷达)飞行。在一维世界中,雷达的角度是恒定的,飞机的高度是恒定的,如下图所示。
x_{n} 表示在时间n时飞行航程的变化。飞机速度定义为距离相对于时间的变化率,因此速度是距离的导数:
雷达以恒定速率向目标的方向发送跟踪光束。跟踪周期为\Delta{t}。
假设速度恒定,系统的动态模型可以用两个运动方程来描述:
根据方程可知,下一个追踪周期的飞机航程等于当前追踪周期的航程加上飞机速度乘以雷达追踪周期时间。在这个例子中,我们假设飞行速度是恒定的。因此,下一个周期的速度等于当前周期的速度。
上述方程组称为状态外推方程State Extrapolation Equation(也称为过渡方程Transition Equation或预测方程Prediction Equation),这是五个卡尔曼滤波方程之一。这个方程组将当前状态外推到下一个状态(预测)。
我们已经在前面的例子中使用了状态外推方程,我们假设下一个状态的重量等于当前状态的重量。
矩阵表示法中有一种状态外推方程的一般形式,我们稍后将学习。
在这个例子中,我们将使用上面的一组特定于我们的案例的方程。
现在,我们将在案例中修改状态更新方程State Update Equation。
2.1 \alpha-\beta filter
设置雷达跟踪周期间隔 \Delta{t} 为5ms。假设在n−1时,无人机(无人飞行器)的预计航程为30000m,速度为40m/s。
使用状态外推方程,我们可以预测时间n时目标的位置:
时间n时的目标速度:
然而,在时间n,雷达测量的范围( y_{n} )为30110米,而不是预期的30200米。预期(预测)范围和测量范围之间有90米的间隙。造成这种差距的可能原因有两个:
- 雷达测量不精确
- 飞机速度改变了。新速度是: \frac{30110-30000}{5}=22m/s
这两个说法中哪一个是正确的?
让我们写下速度的状态更新方程:
系数β的值取决于雷达的精确程度。假设雷达的1σ精度为20米,很可能是由于飞机速度的变化导致了预测距离和测量距离之间90米的差距。在这种情况下,我们将β因子设置为高值。如果我们将β设为0.9,则估计速度为:
假设雷达的1σ精度为150m,很可能是雷达测量误差造成的50米差距。在这种情况下,我们将低值设置为β因子。如果我们将β设为0.1,则估计速度为:
飞机位置的状态更新方程与前一个例子中推导的方程类似:
与以前的例子相反之处是,上一个例子中每次迭代需要重新计算α因子( \alpha_{n} = \frac{1}{N} ),在这个例子中α因子是常数。
α因子的大小取决于雷达测量精度。对于高精度雷达,我们将选择高α,这将给测量带来很高的权重。如果α=1,则估计范围等于测量范围:
如果α=0,则测量没有意义:
因此,我们得到了一个方程组,它构成了雷达跟踪器的更新状态方程。它们也被称为α-β轨迹更新方程(α−β track update equations)或α-β轨迹滤波方程(α−βtrack filtering equations)。
注:在一些书籍中,α−β过滤器称为g-h过滤器,其中希腊字母α替换为英文字母g,希腊字母β替换为英文字母h。
注:在本例中,我们从距离测量( \dot{x}=\frac{\Delta{x}}{\Delta{t}} )中得出飞机速度。现代雷达可以利用多普勒效应直接测量径向速度。然而,我的目标是解释卡尔曼滤波器而不是雷达操作。因此,为了一般性,在我们的例子中,我将继续从距离测量中推导速度。
2.2 估计算法
下图描述了本例中使用的估计算法。
与上一个例子相反,这个例子给出了增益值α和β。在卡尔曼滤波器中,α和β被每次迭代计算的卡尔曼增益重新计算更新,但我们稍后将学习它。
现在我们准备开始这个数值例子。
2.3 数值案例
考虑飞机在一维世界中正径向远离雷达(或朝向雷达)飞行。
α−βfilter的参数是:
- \alpha=0.2
- \beta=0.1
雷达追踪周期每5秒更新一次。
注意:在这个例子中,我们将使用非常不精确的雷达和低速无人机(UAV)来更好地显示图形。在现实生活中,雷达通常更精确,目标也更快。
2.3.1 第0次迭代
初始化:
当时间n=0时,初始条件如下:
注:追踪初始化Track Initiation(或我们如何获得初始条件)是一个非常重要的主题,稍后将讨论。现在或者目标是了解基本的α-β过滤器操作,所以假设初始条件是由其他人给出的。
预测:
应使用状态外推方程将初始猜测外推到第一个周期(n=1):
2.3.2 第一次迭代
在第一个周期(n=1),最初的猜测是上一次的估计值:
- step 1
雷达测量飞机的距离:
- step 2
使用状态更新方程计算当前估计值:
step 3
- 使用状态外推方程计算下一个状态估计值:
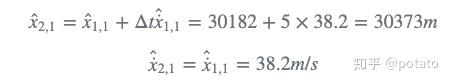
以下是第2次至第10次迭代:
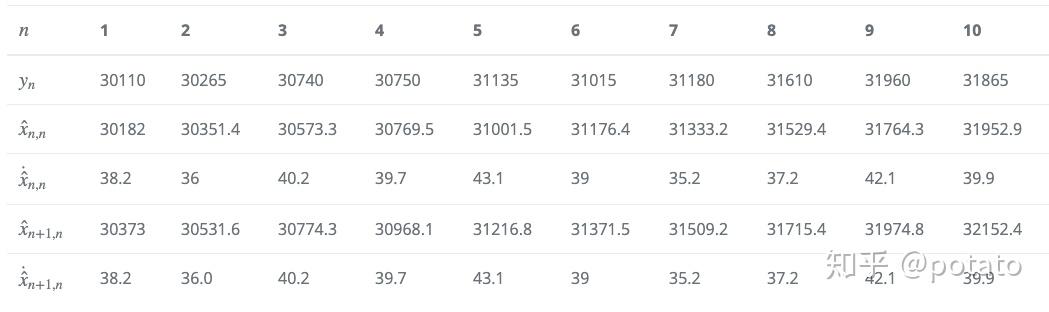
下表总结了我们的测量和估计。
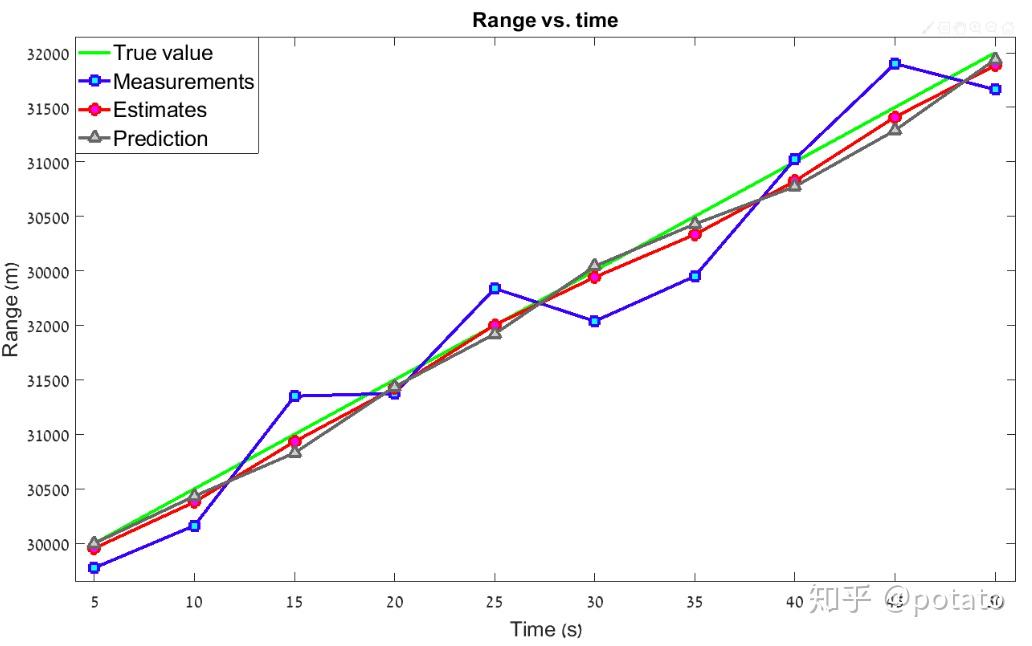
下表比较了真实值、测量值和估计值。
我们可以看到,我们的估计算法对测量有平滑的影响(即,逐渐测量值的变化缩小)并且它收敛到真实值。
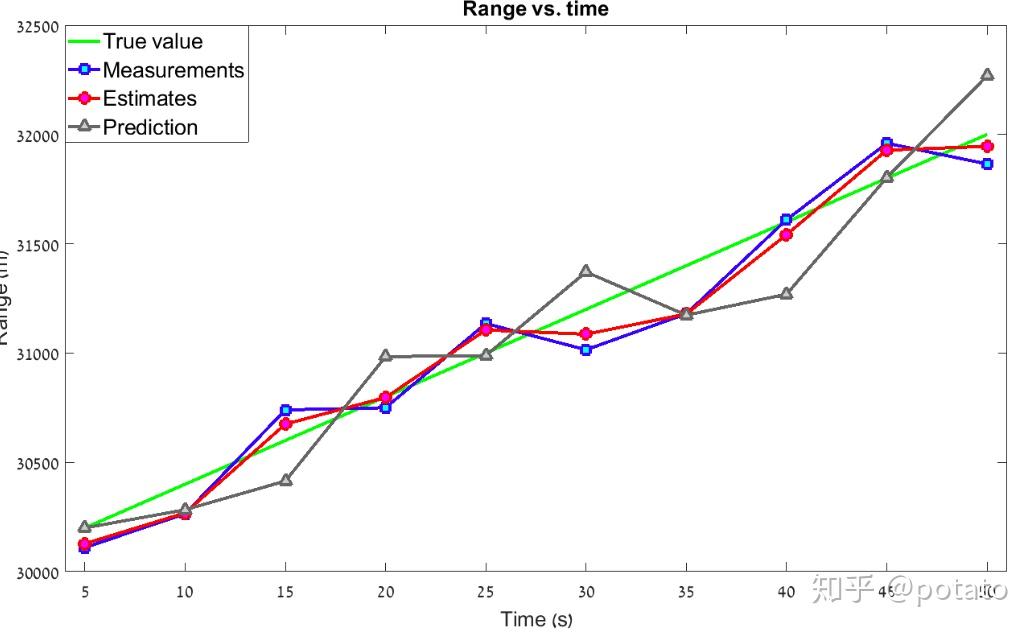
使用高α和β:
下图描述了α=8和β=0.5的真实值、测量值和估计值。
这个滤波器的“平滑度”要低得多。“当前估计”与实测值非常接近,预测误差较大。
那么我们应该一直选择α和β的低值吗?
答案是否定的。α和β的值取决于测量精度。如果我们使用非常精确的设备,比如激光雷达,我们会更喜欢高α和β的测量。在这种情况下,滤波器会对目标的速度变化作出快速响应。另一方面,如果测量精度较低,我们会选择较低的α和β。在这种情况下,滤波器将降低测量中的不确定度(误差)。然而,滤波器对目标速度变化的反应会慢得多。
由于α和β的计算是一个重要的课题,我们将在后面更详细地讨论它。
2.4 案例总结
在这个例子中,我们推导了α-β滤波器状态更新方程。我们还学习了状态外推方程。本文提出了一种基于α-β滤波器的一维动态系统估计算法,并求解了匀速目标的数值案例。
案例3:在一维空间中追踪加速飞行器
在这个例子中,我们将用上一个例子中已经解释过的α−β滤波器跟踪以恒定加速度运动的飞机。
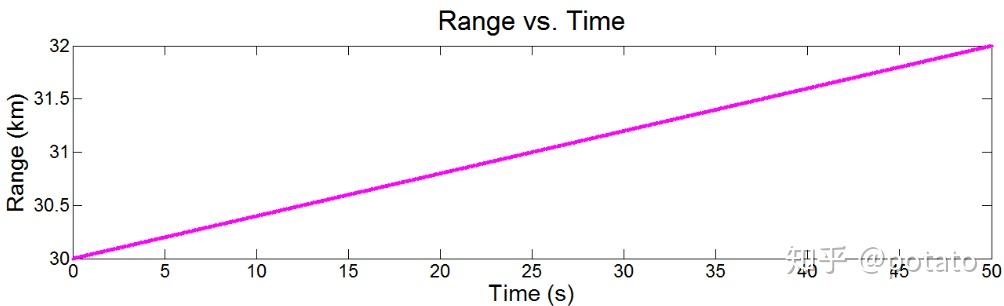
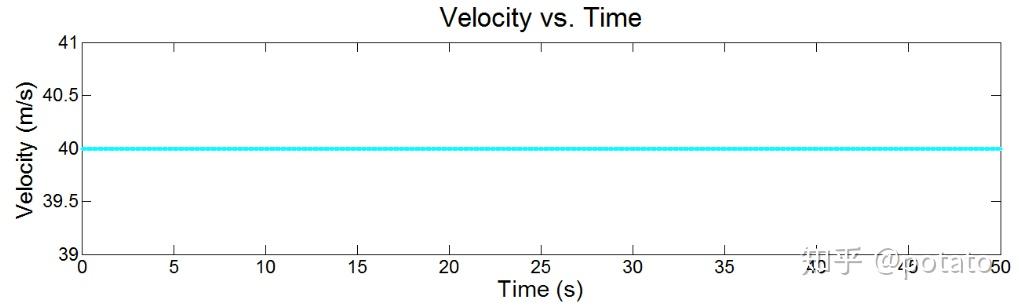
在前一个例子中,我们跟踪以40米/秒的恒定速度运动的无人机。下图描述了无人机航程和速度与时间的关系。
如你所见,距离方程是线性的。
现在我们实现加速飞行器。这个飞行器在前15秒中以50m/s的恒定速度运动,然后这个飞行器在后面的35秒中以8m/s的加速度运动。
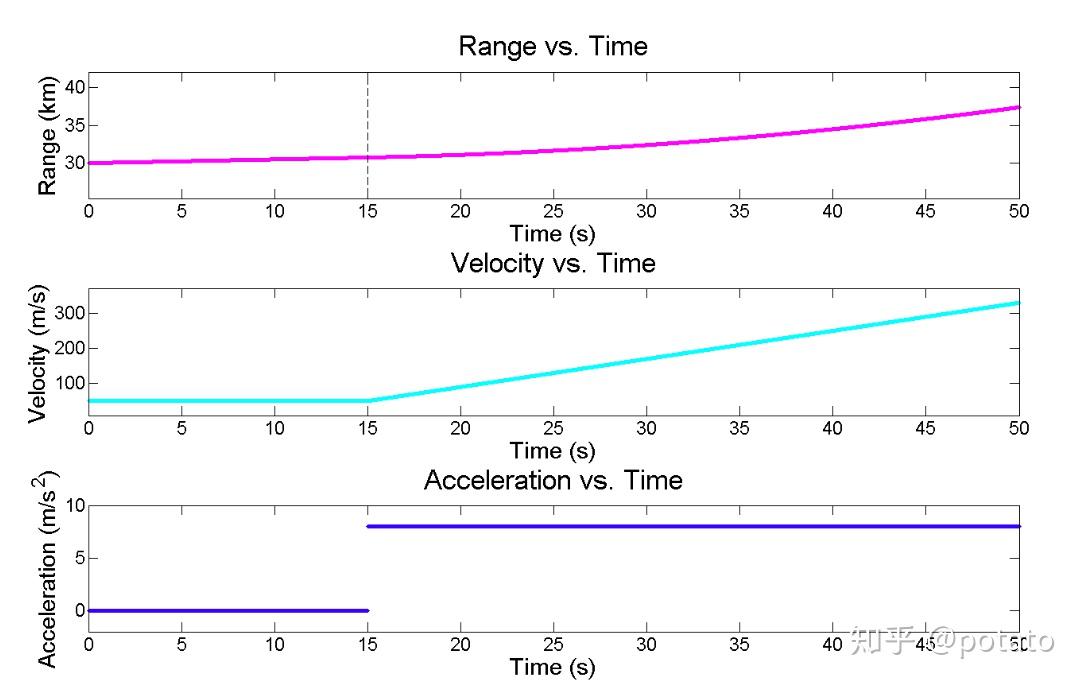
下图显示了目标航程、速度、加速度随时间的变化:
从这张图中可以看出,在前15秒飞行器的速度是匀速的,在15秒之后线性增长。在15秒中距离的变化是线性的,随后呈平方增长。
我们将使用在上一个案例中已经使用过的α-β filter来追踪这个飞行器。
3.1 数值案例
假设飞机在一维世界中正向雷达(或远离雷达)径向运动。
α-β filter的参数分别是:
- \alpha=0.2
- \beta=0.1
雷达追踪周期为5秒。
3.1.1 第0次迭代
初始化
当时间n=0的初始条件是:
预测
应使用状态外推方程将初始猜测外推到第一个周期(n=1):
下表汇总了所有滤波器迭代:
以下图表比较了飞行器的真实值、测量值、航程估计值和前15秒的速度。
你可以看到真实值或测量值与估计值之间存在差值。这种差值称为滞后误差lag error。滞后误差的其他常见名称有:
- 动态误差 Dynamic error
- 系统误差 Systematic error
- 偏差误差 Bias error
- 截断误差 Truncation error
3.1.2案例总结
在这个案例中,我们检测到滞后误差是由加速度引起的。
案例4: 使用α−β−γ滤波器追踪加速度飞行器
α-β-γ滤波器(有时称为g-h-k滤波器)会将目标的加速度考虑进去,因此状态外推方程为:
状态更新方程变成:
4.1 数值案例
我们再回头看一下上一个案例:这个飞行器在前15秒中以50m/s的恒定速度运动,然后这个飞行器在后面的35秒中以8m/s的加速度运动。
α-βfilter的参数是:
- \alpha=0.5
- \beta=0.4
- \gamma=0.1
雷达追踪周期是5秒。
4.1.1 第0次迭代
初始化
当时间n=0时,所有条件被初始化为:
预测
应使用状态外推方程将初始猜测外推到第一个周期(n=1):
4.1.2 第一次迭代
在第一个周期(n=1),最初的猜测是先前的估计:
- step 1
雷达测量飞机的距离:
- step 2
使用状态更新方程计算当前估计:
- step 3
使用状态外推方程计算下一个状态估计:
4.1.3 第3次迭代
经过一个单位时间延迟后,来自上一次迭代的预测估计值成为当前迭代中的上一个估计值。
- step 1
雷达测量飞机的距离:
- step 2
使用状态更新方程计算当前估计值:
- step 3
使用状态外推方程计算下一个状态估计:
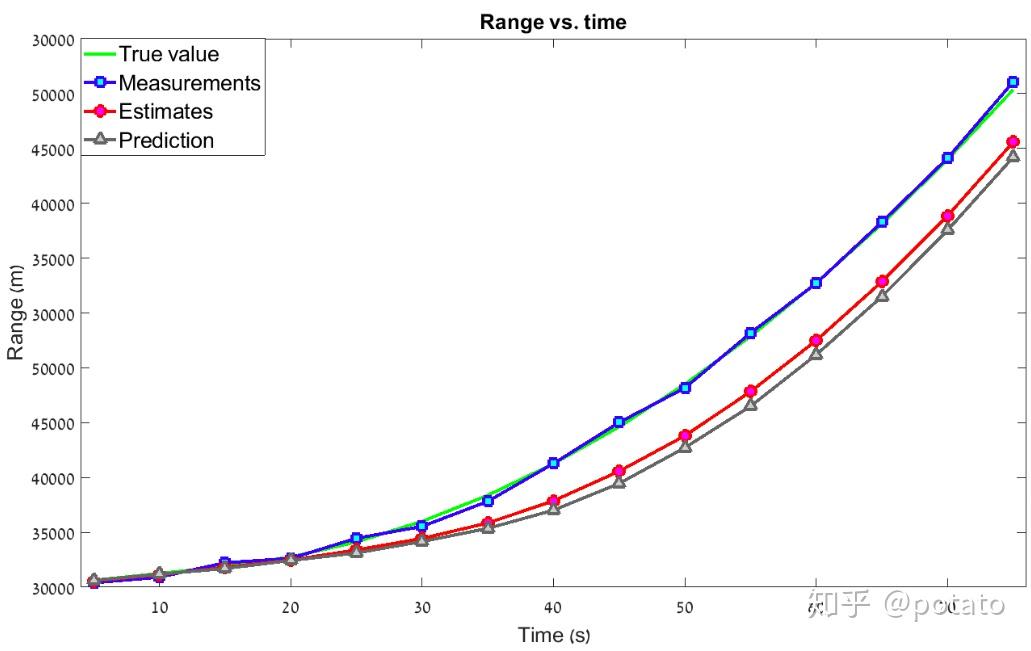
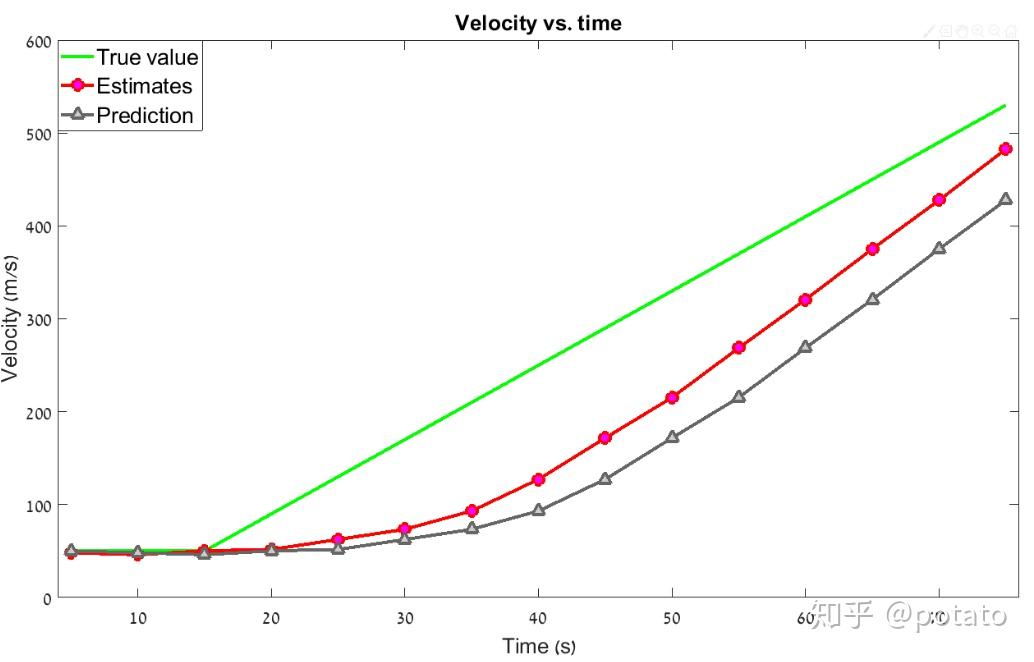
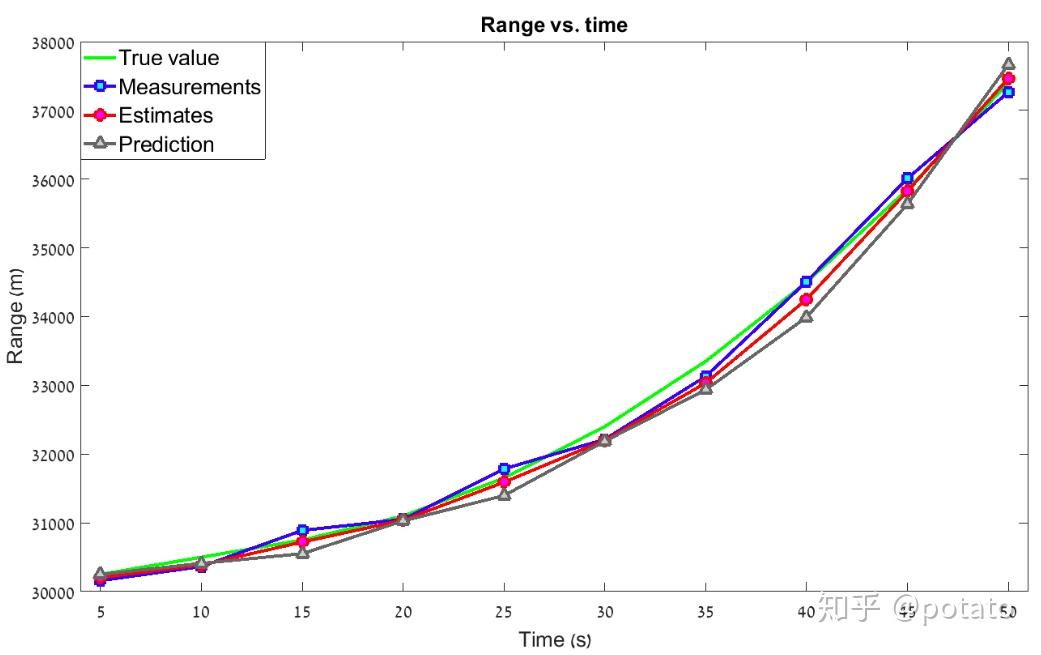
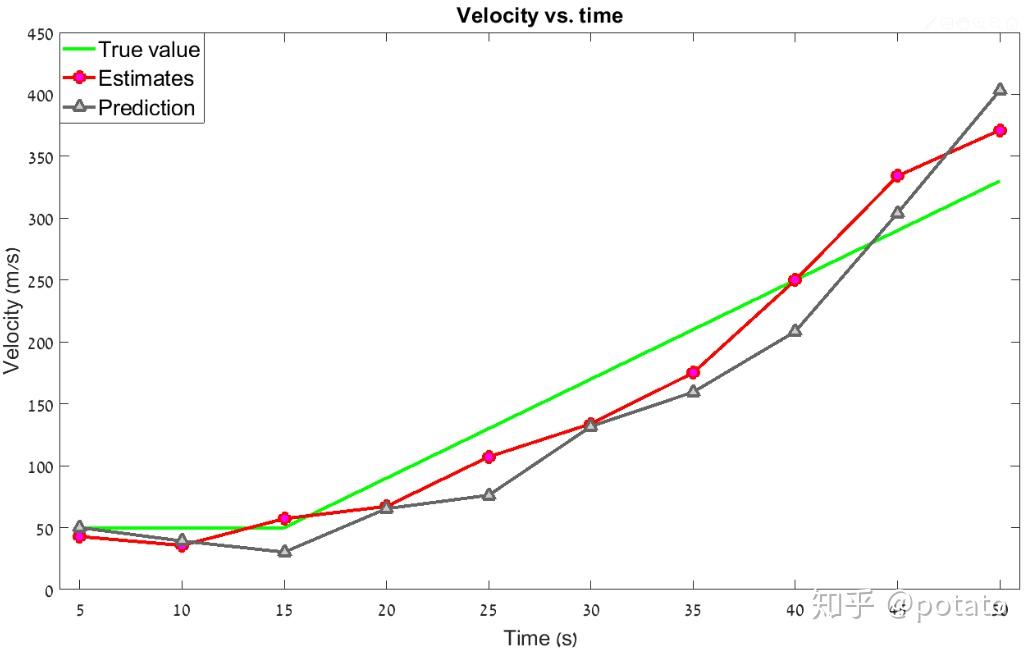
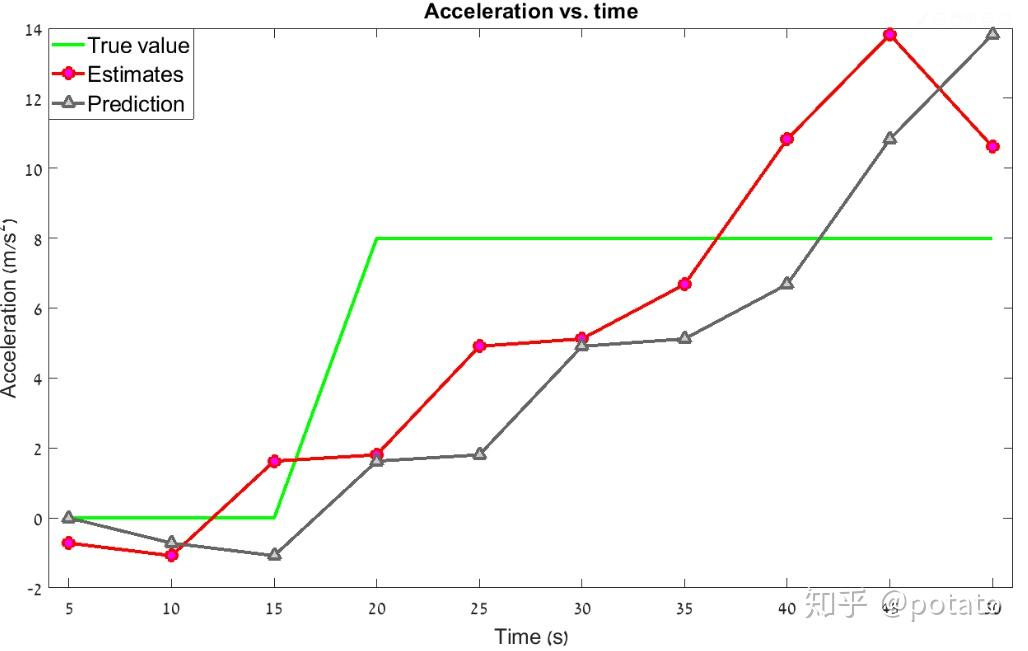
以下图表比较了前10秒航程、速度、加速度的真实值、测量值和估计值。
如图所见,带有包含加速度的动态模型方程的α-β-γ滤波器可以以恒定加速度跟踪目标并降低滞后误差。
但是在目标是高度变化的情况下会发生什么呢?目标可以通过转弯突然改变飞行方向。真正的目标动态模型也可以包括一个突然加速或转弯(改变加速度)。在这种情况下,具有恒定α-β-γ系数的α-β-γ滤波器会产生估计误差,在某些情况下会追踪失效。
卡尔曼滤波器可以处理动态模型中的不确定性,这将是我们总结后的下一个课题。
\alpha-\beta-(\gamma) 过滤器概述
有许多类型的 \alpha-\beta-(\gamma) 过滤器,它们基于相同的原理:
- 当前状态估计基于状态更新方程。
- 下一个状态估计(预测)是基于动态模型方程。
这些滤波器之间的主要区别在于加权系数α−β−(γ)的选择。有些过滤器类型使用恒定的加权系数,有些则为每个过滤器迭代(循环)计算加权系数。
α、β和γ的选择对于评估算法的正确功能至关重要。另一个重要问题是过滤器的初始化,即过滤器第一次迭代提供初始值。
以下列表包括最常用的α−β−(γ)过滤器:
- Wiener Filter
- Bayes Filter
- Fading-memory polynomial Filter
- Expanding-memory (or growing-memory) polynomial Filter
- Least-squares Filter
- Benedict–Bordner Filter
- Lumped Filter
- Discounted least-squares α−β Filter
- Critically damped α−β Filter
- Growing-memory Filter
- Kalman Filter
- Extended Kalman Filter
- Unscented Kalman Filter
- Extended Complex Kalman Filter
- Gauss-Hermite Kalman Filter
- Cubature Kalman Filter
- Particle Filter
我希望以后能写一篇关于这些过滤器的教程。但是本教程是关于卡尔曼滤波器的,这是我们下一个例子的主题。

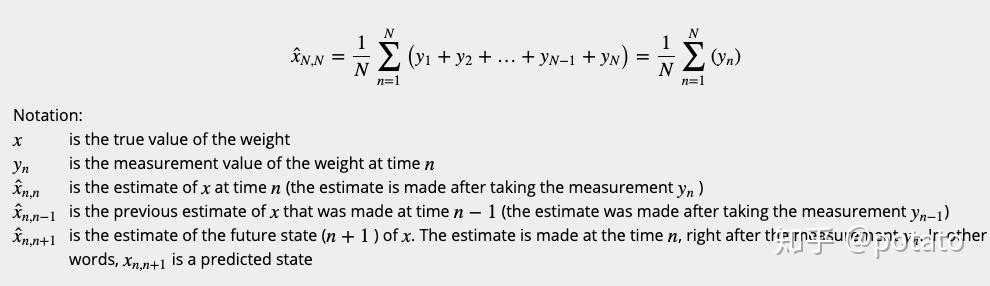


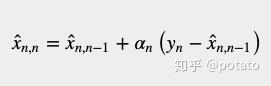
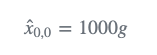
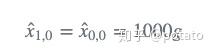
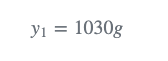
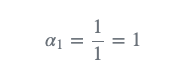
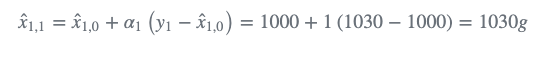
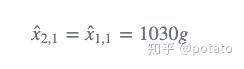
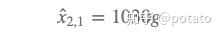
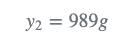
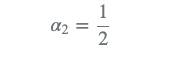

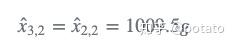



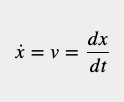
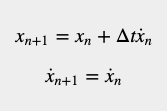

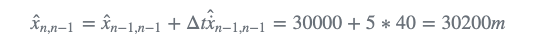
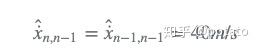
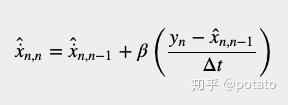
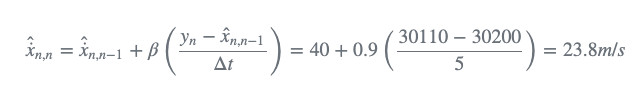
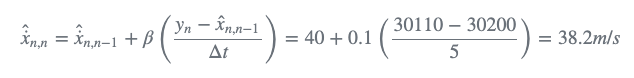
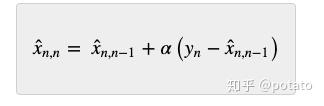
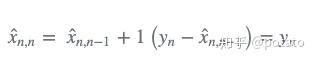
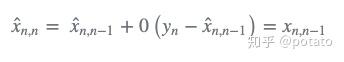


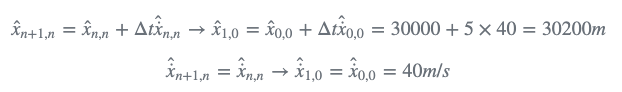
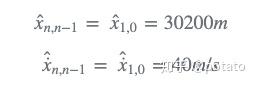
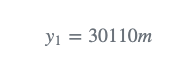
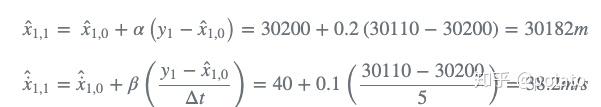






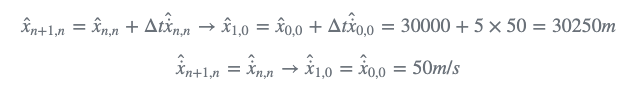




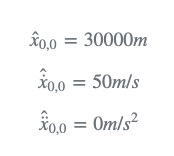
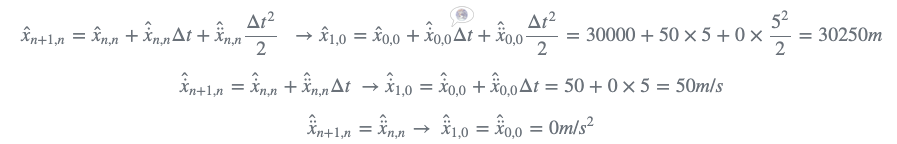
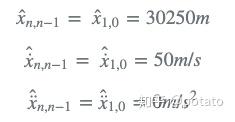
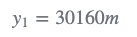
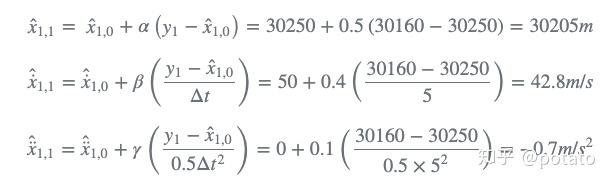
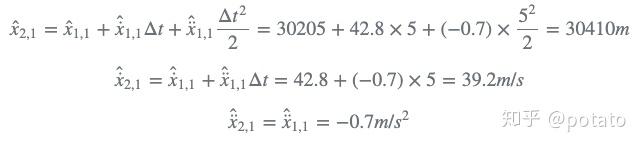
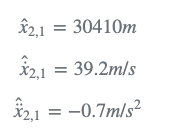
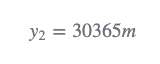
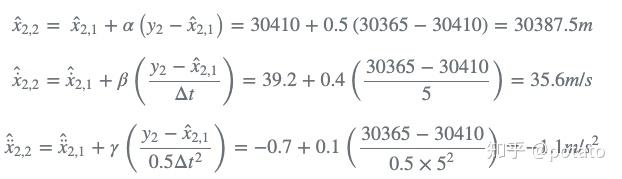
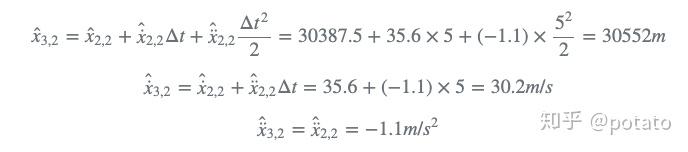



字母上面的尖括号意义是什么?下标里面两个字母分别表示什么意思?
文章写的那么清楚
请问2.1里面的速度更新方程为什么不是X*n,n = X*n,n-1 + beta((y-Xn,n-1)/delta t) - X*n,n-1)求解惑,谢谢
速度残差 = beta*[ (Yn-Yn-1)/dt - Xn,n-1 ], Xn,n-1上面有点![[好奇]](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEIAAABCCAYAAADjVADoAAANVUlEQVR4nO1be2wcRx3+Zvfs9d7D5+bOlzjFj+BHG6d2mwDFRonixiEtUYG2gFohNZLrvlvxkAj80ZRKffAHRdCCKxSSUpGAKEoRSVvUBwlxaFQHlZbUbkpqJ+RiO3bss0Pse3l9tzv8sZ692b3d89m+IP7wJ512dh7fzHz7m9/Mzs4By1jGMpaxjGXkC8Lf7OsQQn0Dwq0AvkQIVlGKiwDeePZ4+teFrnhfhxBqa9FKAaD7hDC94yVtvNB1LASGEPs6hFDvgPABIeRqayZK6YXmem3DYhq7r0MItX5Gayr14TZRQDkR0CKKQrVdXlXVzmsqzmkUH01HcbDnfaHvfyUQYY11EiGTkR7/8TvpTfkSD3ShvawUuzRN3CyVUDJ/CXukZrXu1Cz57ep76YuL5cgHBAB2bnTdA0IyFVHaef9d6fO/etlVTYEnmUD335naWv8ojjiR7esQQl/aot2nqeJTuTrv8jWgRA6Y4maSkwCAdLTftoyqauc1DXuSCfyh6gGcyb+L+YEAwPc3ud6hIBsBAJR28j7hextdzxFCvq0n0ed/cjz9HTuigS60r7gKL9qZvb9yG7RgHYTAmrwapU2eA4mOIzHWmyUME6T8bjyTZx/zggsANIo1ZO75NdVrr+N4JgMBenMRDO5GnSxjT1Gx0MbHe0OtIFevNzovLKBRQmANEFgDT83nASUG9ZO3ERvvAQCIolAtinh68nfaffEYthbKOgQAEAjOAbpT5J3Tvg4hRIEn2b1VlIEutHu8OMyL4A21wr/pCYjNd+RtATkheSE23wH/pifgr9xmRIuiUC1JYn9kPx5beiXcrDHQhXbeSw90oX33y67fMP9gnTki+/FYUZHwNE/mW/9wYTqfC0oM8ZO/Nw2ZVErbdXkKJ6QinF+shdg6NKvzpJRe+Nbd6TZWiVUEb6gV4jXbAMkLKDHzdSmwcimxTFq4B1NDb+vZZgiVSihRZgh1FamDVMOJRAK7FiKKrRDf2+ga5i0hlwj+ym1ATWs2ibXhi4WVh7uPn/w94pEBalfMVaQOLsSpZvmwnRtd91iHAxNhoAvteYkAZDd+IVc+bBWTu09E43rWEkoCVS3EU15P2LSdTolVmio+Nfk7hAd3o86+kRnM58xfYT5hcDfqVlwFY7jYiuDUMdb4fK/WsB0nB2WGUCFYD7luK3zrH0agqsWw9HRKrPJ4cXg+MbKEaKrXXgelr4DSV5rrtR+xeFnGHrZG8IZa7S0hV8eWChvOFaEqIxz5YD9NnjkMosRArl6P8g13E1Ky2rAOSRL7c4mR19J3ZC/pdHvJXnbv3/REVp5LwxMYDU9jbMys7cqVGipqSrHiU8F8qlowX+SdvaAzI4afkEooYQs4AEieOWz4EVeROui09sgSYu4N9AUAaKrXHmlr0Uo9Xhxm1uBb/zAEb7mRX4tF0P1WHMlYMmfHZK+Mtps9prJ2WBRfuAeRoVMmQQJVLYRcvR5Athh/PizcaH2ZE60V1PvEN0HILSCkcXySrGlr1YIul3AHMDdNrm428l4ansCJY5lGy14ZpZ9uxcqGz6Osch0ETwCYiSA9m0Z6No0z/0ogGCSQS922nVs0X9U1kAOVkAUXSU4N652fGoanrJpA8qBoxaeRnBghSEehaYK/bo0m/+Qg3uDrzrKInRtdB0DI1/VEevwHD6Yr7ayBf3KyV8bK5lsRqN2AYndpVgdH+7ox1vu60cHW9vKsoXJpeAIn/x5bMh8/pfJWQZQYIh/sNyxGUdQGfojYOctHCOhxAnp85/3pN5kILl8DBG85tFgEAEwirNnyECqa2mwbDQAVTW1ovP2HkL0yAODk32MGD7vyIiyFj4cQrDfCVPKaZhNZxh4+b05nGdmHo+w9orRxB6jkheAtx6XhCfQc0Suu+cI3EAn34cx7rwIA1rV3YlXD5+CvqM3imxo9i49f/alerlbC2ht8Beeb/Ochw1cEWx/K6h+fzluFy0mEwd2oYyK4fA2gc/O3FotgNBwFoI/hngPPoL+3zyjX3/sd+ANBfPPpQ1mN91fUwrP6WsRHTmNsTMDaK8DHOsmmTqLEQCWvcV0RqsLk4Ihenxt3AvrK03FB5RLJZhb2lNWY0sJnFQDAvz/50NRohqnJCRz55YO2vNWf3Q4Aplmh0Hy5wA+XeFQ0VsmOQhRL9IssTH2rbPOMXRh1rNCuQwAg+zPT5+XLZsstBB+zBDozQollQceswlNeTwBAdoMOdKEdyCFEKkWuY2HKLWv5xk9NTjg2HABmE9M5068EH1ttJhMgiaETADICsDBv4Z4SUgPkEEJ2k3WA7h94lJVlXvb8AefVoj8QtPX6ySmzdy80HzN92Q06cX4AiaETwGwCvHVQSedJJkCY5dsKYbcmZ0REiRnT1g03brZmM7Blxy7b+MTEkBEuK6MF56OSF+XXfY0kEyBMjMhHf6QkejFTqFhf0MluGE/BVgglBWMDtkQOwDrWVq7UdCKvjNu/+5zpSfoDQWzvfAzXbL7LtuFjva8D0Kc7xltIPqLEgGI3qq83XBySCRBViWaVTSZAKMVKIMf0yTCTnIQburmxhjeuJQif1T21MB3BQy9+hNG+briDlZD95Y4LodG+bsO7N67N+IZC8+n+YBUCVS1k+PQJ9uRzrpnm3Vy2fn9gqKmVAADxkdPofe0XCNRugL+i1rHRnxx7GeF3D5jKXik+9sDYt5JkAkSUfKY8yYRZmAVZBA/9CUgIn1UQHzmNj//0ZNb7wWxiGpNnP0Ak3If4yGkAuvk3rs3eXSs0H5DZwQIsS4DZhBEkBGOOQkhFOO+ojEPjk7Ekwu8eQPjdA4bzsy5yamolNNbGAdi/fRaab26VSYyhMScAUTLTsKohAjgMje4TQvaEPZvIKMmFG2uT2L5NM5lnMpY0NVr2yrhxQ8oYxxMj0QxPAfjs2keiFw3z95TX6yIUZwumpshJwMEidrykjY9tFqlUQkk62g/Mzu1BFLszlbHw3LWxNonGWmBiQjVxBYMigDgAEUdefQ9vv5X5HtHQ3ISvfnnNXB7kz1dMgVluK4Urx8Lxscy3KMPPzbU9fjlspMVnaBjI4SwFQT2WFcmNLdPT5Bu62odgUDR+DEfePGWIwKbH/t4+PPvMqyZTNQk91/EsPru6LWHePwil3Ef+Yrcpred9oQ/I4Sw1io8AtAH6mGKrsXlhEYYhPKqb+rabG9B+yzpMTKg49No51FQo9twOPPmAKNNIXNLfMN0rVmfxsjSpRDu14yU6DuSwiOkoDrIwb0qLRU2F/obJBAkGRXR21KH9lnVL5raCb6/b5zGladMXjLAg0qNG2Ims/lEcUWYIBTJnFpgJL+Z6/WevBaAPhx89/Y4x9pfC6XTlTd+6hXBpfNAI8w8794KKqC+wIFOSDRPTuJ4nHgDKfXHsfOwrAPS3TN43WMvy94upix8W1nwsDdAfdl5C8IrFxnuMscyIrZXwvsTOr3z4j9NGuKG5yeCwcvL3ufjt4iNDp4z4XMNC9qhdfFpOIeofxZHUrNZtR8SLwBphjePDkajHmDW23dyAe78ZyuqEEyd/tea3luOfuHtls8l6nIbFvEIAwOVpGNtZ7NQKa5C1EU4WQZRpHHrtnCHC1psqTXVYn77TMLFL46+8NQSr67PS+dnCehZsXiGsVmGdQZzGqV0aAFxfp8epShSHjw7h8NGhrDx8OSqVmizRysnEVpWoyRqsTpIXiWr4mbXOeV+6ACCZxH2aRvrZSlOVA7C+zc2HmgoF/b3Asy9chD+QNm3L3fSFMkc+okznrEubvgBR8pnM3rp2iAydMllDxT3ZRxXzOuNV9QDOCKL6OLuPjfeA3+iwbnrY3W+9qRLbbta3/ZgIDc1N2PnIqqyO2m2iONUnSj7EL4dN1lBemVmb8CIAQCpFb7Pr44IOgk7sx8uuIuFOdu8Ntdp2go+zu59JTqLEwar4/Cxs5bDmO//hX4z4T13bYsRbRfD41F1OJ2iyPgLnwnVlwt+qVtPtRUUkBACz8WEUlYQguCSoShSCSzKF+Y7w98UlZaDqLASXZHSKT7d21MrJ1zM5egapZMZCij0ypiIXMBH+0BxfrN27qgPPO/VtwUeDB3ejjj8mAGQsw+4J5rKQ+cJOFsGGRmy8B8oModbdJh5SiXYqlqDfznViGFjYOVAAur+Ix7BVVTVj8yY23oP45XBW43nY3bN8TmWsYHlZnYB+MMQur8erdhcXa/dW3EOvm08EYBEWwbCvQwht36L9nPcZ7Iy1nSB2TzjX1a4MoG8d8mcskwl6KpWitykpVLOPNWmVHlvoectFC8Fgd/AUmDtnVUBYBQAARdG63uoWnirEXxmWLARg7zcY7E7iLwT8apZBVbXzl/6DznxMPl8URAiGkb2kU5Lp405/TOE/Hzr9TQFw/quCMkOoIKqPv/FXYU+h/9BSUCEYRvaSTiLgu+z76VJxJQVguCJCMAzuRp3sxp2g2Gr9G8N8SCboKUGkR6ejOFjIIeCEKyqEFewsQpkfLZqGVaKAckD/tiAIuJhSyMW0So/9P/zZbRnLWMYylrEMZ/wXencHIEogJOMAAAAASUVORK5CYII=)
![[笑哭]](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEIAAABDCAMAAAAf1iN/AAAABGdBTUEAALGPC/xhBQAAACBjSFJNAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAAjVBMVEUAAADvpgDvpQDvpgDvnwDspQPupgDupwDupgDupgDvpQBbi6dai6dZiaZai6ZrjpTvpwD0sBX1uC3/wUD+1WX/5H7/7Y7+3XL+0Fz+x03/6Ia9jTiseSnpwl91PQWGURSVZirXp0XKu3ahgl2xooB8lY9cjKdhmbdws9l/0f7t7e3g2tTEsZ3Sxbj///++rKDQAAAAEHRSTlMAIUBlEKDC74XfUF/nHKWQlKTTgQAAAAFiS0dELlTTEIcAAAQ2SURBVFjD5Vdtm6osELbsxc7WOai4QihgKnba+v9/77lmADMra/fbuZ4bWmGYuZkZcIUg+F9gNg/DMJzPFz+yXoTLFemxXkXz79oPzD02y9n7BNHam8UJIPbd1a9vEcQpzT49cpY4kjc8mW9QlV/NPRxL9Cq3ETrA9p+PkCHJZtKRGWaRPyZAEkxLOMEAQSTZ5+ceyxgo5RjMJEO63+/3n1jHsBx5/JwDGfjI6AGecyyAge3fACbkUT4i9CG7K1CdqS/Asb5flxDykGWg4Kt94s/BdyGW1aNEJNnboA/SsSQkzt+nyNK7UGa4p3NbclEI33YFalYWosy86C4UdCIH8ywXUkqZ574L1fYKKaUqnYARQuYjJ5gdKhUw6Nz6Y3lsO6tgRAonjAlZ3jvhXFDCzzuwR0HpHbFurAcv7YYQjnJgKGg/+y1AUinkgGY83F9z5wQyVPkkIFCFk6TDhC4JSXD4NUOeUyVlgQ1CSB/JysYBg5AGWglRlXlOsfYPJ0U/cKJBJAtCCM0phFG4lEFKMGuOw8YIS1XlOawMyJLrDsVUUAhDlV7VZh4dwFL0Yl3mBXhL6SAZISEJpbSSsrKqSmnYHYpRSnP8CSt11ExKTSllhGyurzlQMK0PNW4eMAUjQakjQUuYBqj1QWjoQD6vC1IdmrY1xhinSin441qUUt2LhZTaGNO2zaEkhLhXbYnGxpiu60zbm1UVZddO32zbrnP6pnYUH1swPh7/AoyhDApaMIod/8R2aQzoHY9HZPoAht3WdH89jqZlCNr/8XAdasyxV+/MdhcEwe8bBlOyF2isG57jdxAEQ4kxjZ2P9o9h9RzdwGIbBLuBoPNhTKJsb0x2we7qxdG0L8NAjkE6jNkFwdb3bSKElEqLquJjQ15WotCwwdnBXG22QRD88W51kAjhdjFsR62LQohCFEWhlfJSqfg1pTadwdZ0R/ShZZyp+vR1bnTPcwNdN5fTWQrGWmvjFhU2BqItOeNafZ0AX5dL09R1rQF1XTfnix04aVlxztyGtgxBsPhojWkPnHHOK3k+TeIiFQfNQ9u27Z/d8JMcc45D3o0n+FLgBGim15fM/dMhKUckUoLXD83PTa1kYfX46DsC/z1jNyT8etRNcz5fLpfL+QxpcWui3FTp6Gs2dIMXcgIqcVrk7niwQg5bpjgqp5TcZgK/qms47/I0hd9TDlXhOE/TR8ctOOUkliFNxWMGnQwYNven4BVyWDfT5JEjwhOk8X0Y/YkvRYBWNSJRRT/Gn54a7dnXRoKoCu0XWFRp70I6dXZd4x3iFkkyEqSvT9BjjjHlJIPjIMkEQ/yCIQgWSzJFggTrVxe9cPOMxF3R3rhazZbuZhcjTeKS6q54m/fump7EEsVxfL1nhm8RIEm0ub+nrlffvO3OwtV6YL+Jwh/duuHKHkVR+Gv2s0v7P4b/AFnBGVPCxsYaAAAAAElFTkSuQmCC)
首先感谢楼主这么清晰的讲解,对于2.1 速度的更新公式中 速度的残差 有同样疑惑:
我能理解 距离残差的一阶导=速度的残差,但是这里的dt是前后两个时间的跨度,那么dt对应的距离残差是不是也应该是发生在两个周之间呢?但是 dt的分母 Yn - Xn,n-1一个是当前周期的测量值,一个是当前的周期的预测值,两个都是当前周期的值,如何对应dt呢? 如能解惑,万分感谢
https://www.kalmanfilter.net/
终于找到了一个能看懂的了,写的很好,感谢!
讲的很好!
2.1 时间应改为5s,或者速度改为40m/ms。
感谢知友的讲解,好多之前不明白的地方,想通了。
括号里最后一句话是想说随机噪声不是内部误差?也就是说他是外部/非系统误差?
你好,请问α-β-γ滤波中的加速度状态更方程中分母0.5是怎么来的?
高中物理
是Δs=aT²吗?