相机(RGB&DEPTH)畸变矫正的通俗理解
相机畸变主要分为两种,径向畸变与切向畸变。
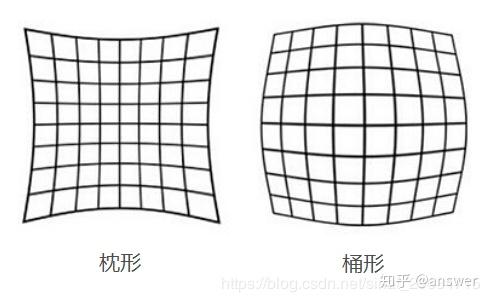
(1)径向畸变(枕形、桶形):光线在远离透镜中心的地方比靠近中心的地方更加弯曲。
上图就是径向畸变的两种形式,其产生的原因是()。
(2)切向畸变:透镜不完全平行于图像平面,即sensor装配时与镜头间的角度不准。
本文主要谈谈径向畸变模型以及深度相机畸变模型。
- 径向畸变矫正
很多资料都介绍了径向畸变模型,很多都是上来就是模型公式:
不懂的人看了真是不知所云,为什么畸变模型是这样的,而不是那样的,本文我将用自己理解的方式介绍一下径向畸变模型的具体内容。
上面的公式 \bar{u},\bar{v} 是畸变图像中的某点像素坐标, u,v是矫正后图像中对应点的像素坐标, u_{0},v_{0} 是矫正后图像的中心点像素坐标, u_{1},v_{1} 是畸变图像中心点像素点坐标, x,y 是矫正后图像点坐标在横纵方向到中心点的像素数也就是图像坐标,所以 x^{2}+y^{2} 可以看作以中心点为圆心的圆的半径平方。那么这两个公式是分别求图像横纵方向的像素偏差补偿,补偿系数为 [k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}],可以看出 补偿系数分布服从二次函数,其实补偿系数后面还可以有 k_{3}、k_{4} 项,在实际应用中前两项够用。
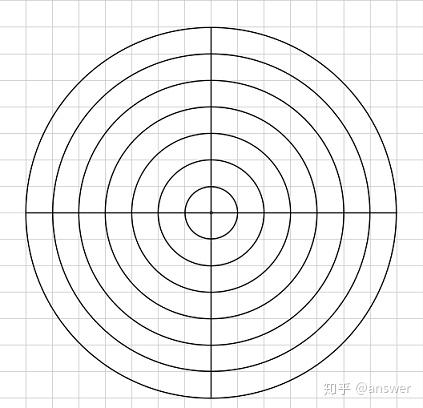
对于该畸变模型我的理解是以图像中心点为圆心相同半径的点补偿量相同,不同半径的补偿量有服从二次函数。如图所示相同半径的圆周上补偿量相同。
所以畸变模型可以写成上面的公式。这里再做一个简单的拓展,如果畸变分布不是一个圆而是其他形状例如是一个椭圆,那么补偿系数 [k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}] 中坐标x,y又服从椭圆分布。具体形式我没有仔细推导并验证。
- 深度相机畸变模型
深度相机畸变有两种,第一种是与RGB相机相同的畸变,如上面介绍的畸变一样,矫正的是二维平面的畸变,矫正方法可以使用棋盘格,为了清楚观察检测到棋盘格角点,使用深度相机采集的红外激光图像,红外激光图与深度图是相匹配的,例如微软的kinectv2相机采集的红外图与深度图。第二种畸变是深度畸变,如果使用深度相机在一个平面上采集图像,理论上深度图像每一个像素值大小都相等,采集的是一个平面,深度图的像素值大小代表深度。但实际采集的深度图不平整。深度图边缘畸变较大,生成点云如下图所示。
形状像一个碗。
- 深度相机矫正
- 直接补偿法
该矫正方法首先认定深度图相机中心位置的像素是无畸变的,那么取相机中心位置的像素值作为畸变矫正的标准值,深度图其他位置的像素值(周围像素的中值)与标准值做差,将差值存储在一张表中,那么在矫正其他图像时,这张表中的值作为补偿量进行补偿。该方法需要矫正时相机到标定平面的距离与实际相机的工作距离相同或接近。
- 相机矫正(修正)

x,y,z 是相机坐标,其中 x^{'} , y^{'} 是归一化之后的坐标,此时 z=1 ,也就是距离为1。
x^{'} , y^{'}为理想条件下的坐标, x^{''}y^{''}是畸变后的坐标,所以说畸变是在此处发生的。
那么畸变矫正是已知 x^{''}y^{''}求解x^{'} , y^{'}。
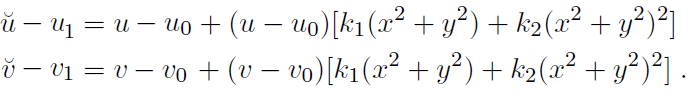

我的理解是,做畸变矫正时,相机内外参数均已知,假设使用棋盘格进行标定,那么棋盘格上的交叉点可以通过投影(内外参)来得到实际在相机中的像素坐标,这是一个线性变换。这个坐标是没有被畸变污染过的也就是所谓的理想像素坐标。
这个变换的确没被污染,但是利用四大坐标系映射还是需要输入输出,输入是镜头给的,镜头给的raw已经畸变,那如何得到理想坐标再进一步完成畸变映射
要求解k,就要同时知道校正前后的像素坐标,可要怎么知道理想的像素坐标呢?从图像上读出的是畸变后的坐标啊,相当于两个方程四个未知数。
如果径向畸变参数公式中有k3,两个方程式,三个未知数,怎么计算k3
x,y是在哪个坐标系下的