60. 数码相机成像时的噪声模型与标定
本文同步发表在我的微信公众号和知乎专栏“计算摄影学”,欢迎扫码关注,转载请注明作者和来源
如果你对摄影有一点基础的了解,可能你经常知道的常识是拍照时,在保证图像曝光合适的情况下要尽量用低ISO,因为高ISO会带来高噪声,就像下图所示
另外,现代单反的传感器一般具有一定的动态范围,很多单反都可以达到2000:1的动态范围(参见27. HDR - 高动态范围成像),当我们获取RAW图像后,可以自己来做想要的色调映射,而不是让相机内的图像处理器来做。但此时我们通常会发现,如果把图像的亮度映射的更亮时,图像上的噪声也加强了,如下图所示,左上角是相机不开HDR时拍摄并保存的一张图像,左下是做某种色调映射或亮度拉伸后得到的图像。右图则是局部细节,可以看到噪声非常明显。
这就让我们不得不问几个问题:
- 为什么高ISO时图像通常会有更大的噪声呢?
- 为什么对单帧图像做色调映射会带来更大的噪声呢?
- 为什么我们之前看到的多帧融合来做HDR时,不会有这么明显的噪声呢?
今天我想通过这篇文章,为你介绍一种基础的成像过程中的噪声模型,以及获取这个模型中的各项参数的方法。通过这些介绍,我们能部分回答这些问题。
一. 回顾图像的生成过程
在2. 从入射光到JPEG相片-数码相机内部的秘密中,我们看到了成像系统是如何把入射光变成最终的JPEG图像的:
那么在这个过程中,噪声是哪些地方引入的呢?
实际上,真正引入噪声的地方就是上面的绿色框的部分
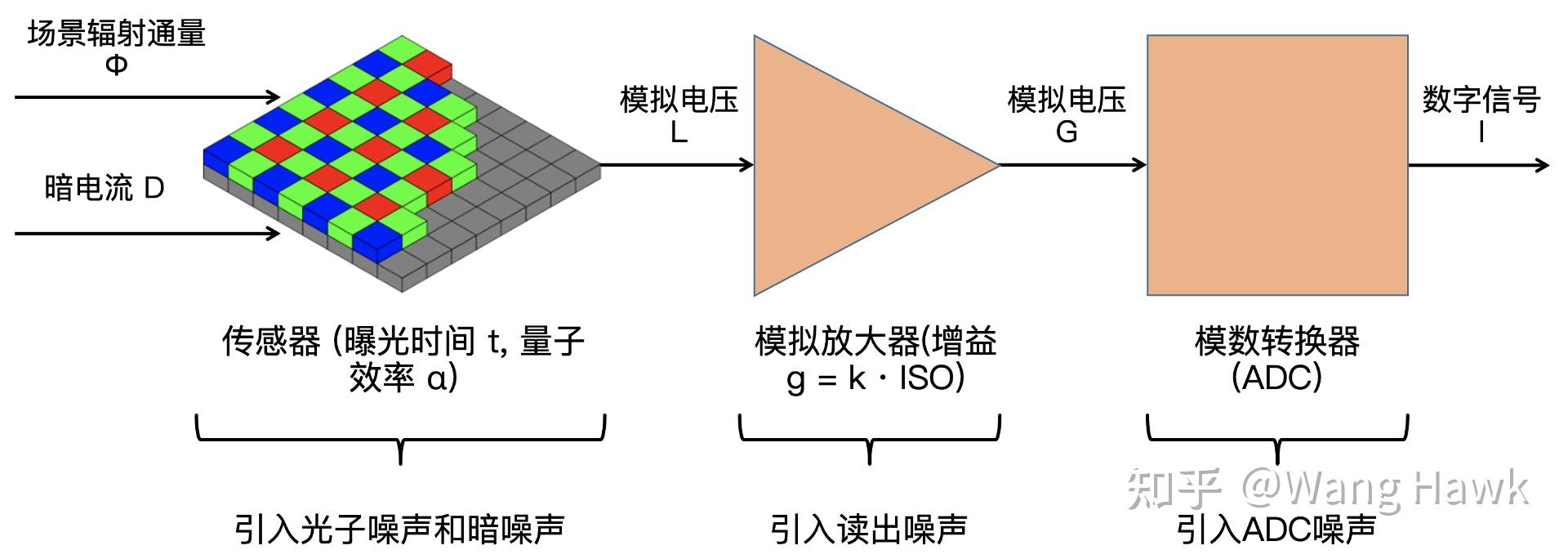
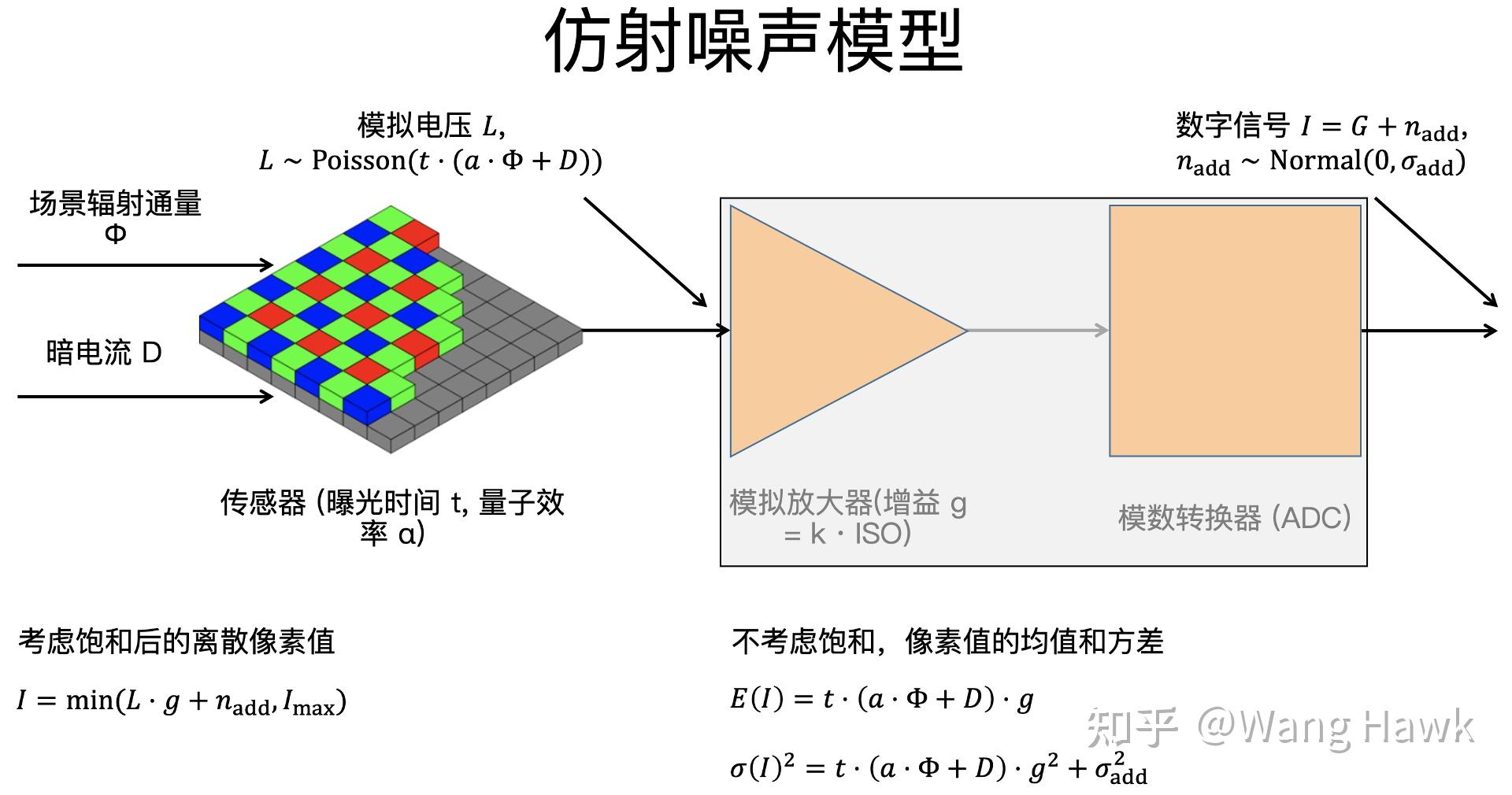
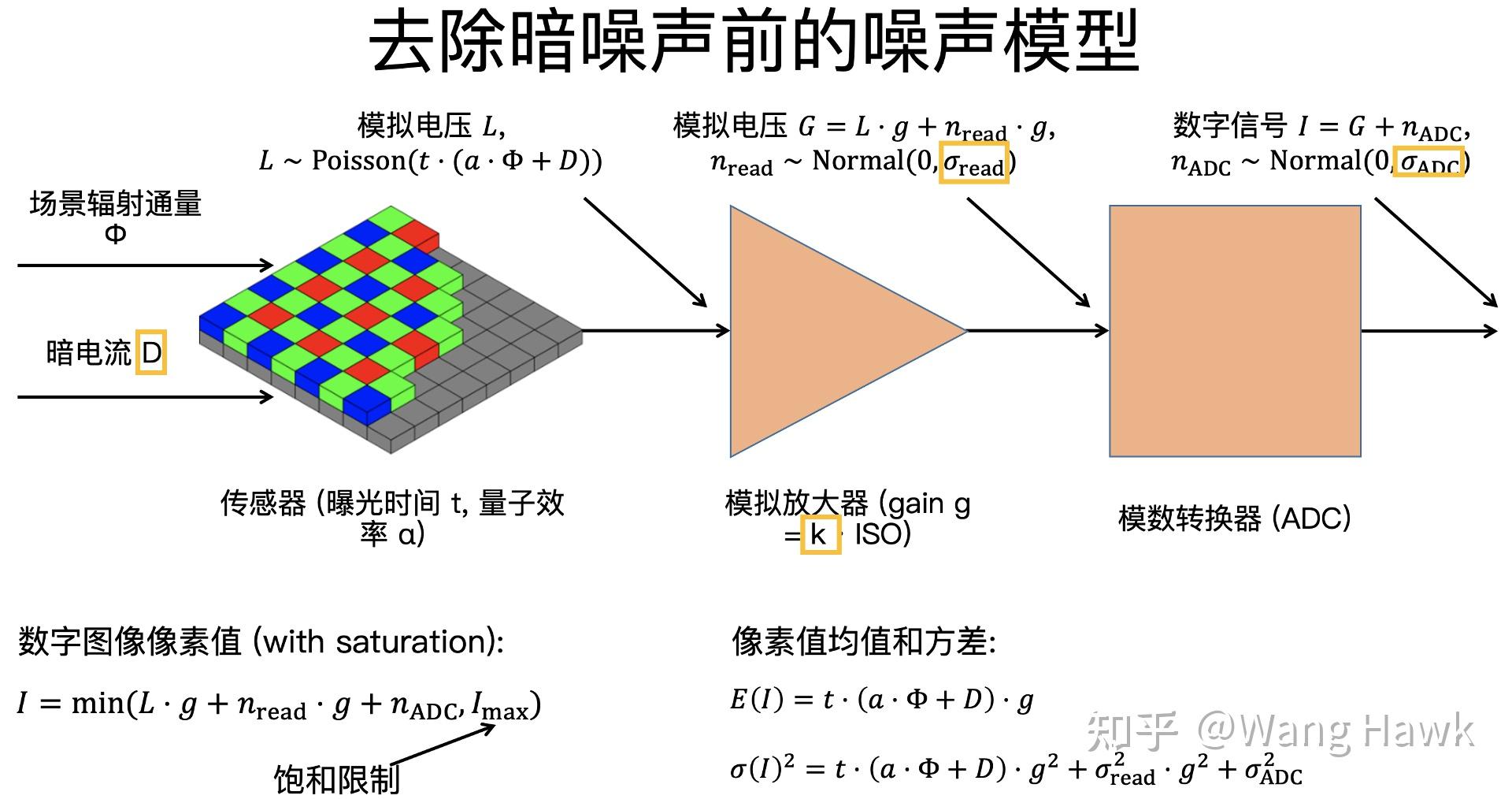
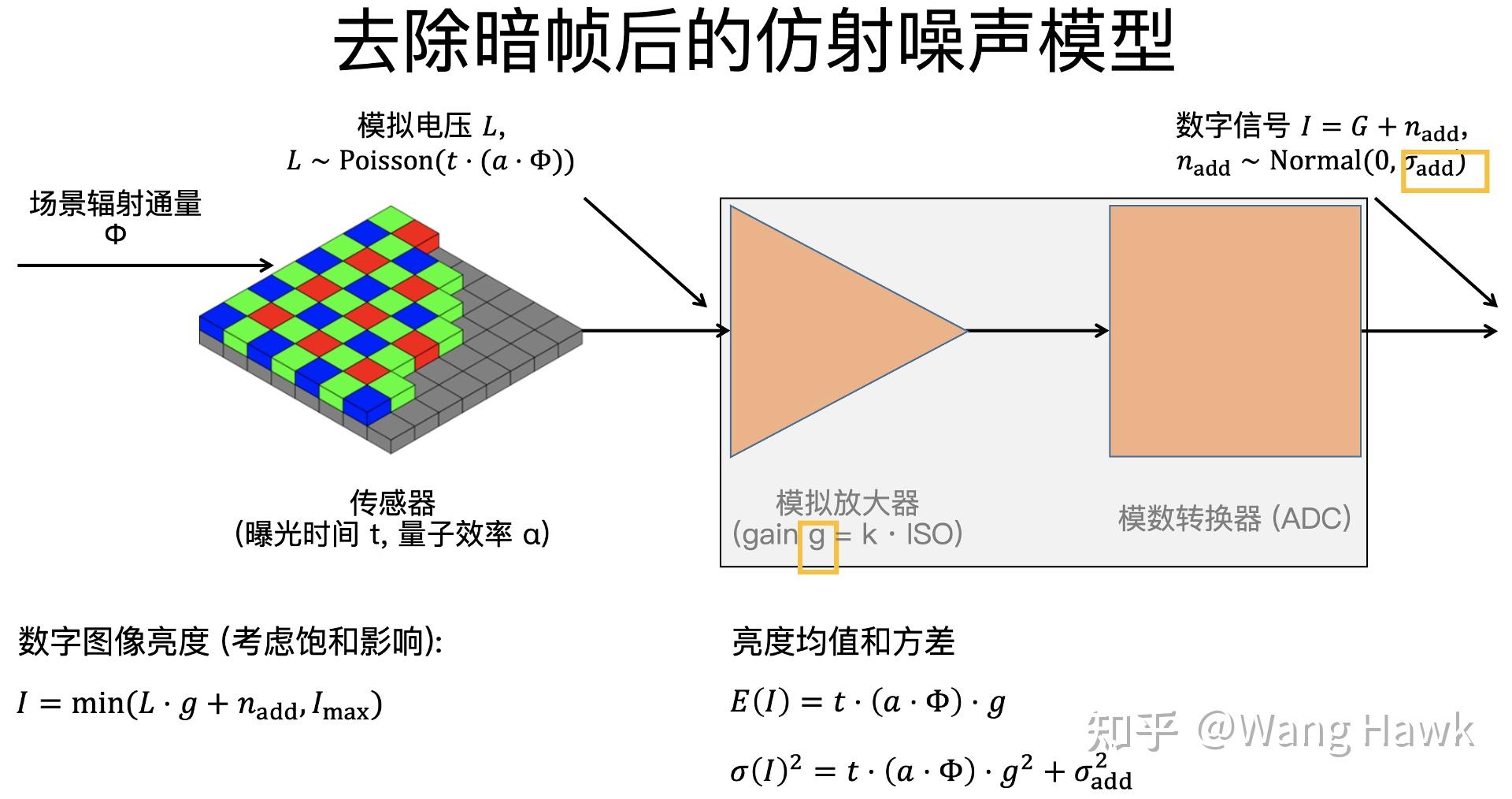
让我们将这一部分进一步拆开看看,噪声到底是如何引入的,如下图所示
这里面场景的光辐射通量是 \phi ,它照射到传感器上通过光电效应产生电子,与此同时,传感器自身因为温度等因素的影响会释放出一些电子,它们构成了暗电流D。光辐射和暗电流共同作用到像素上,产生了模拟电压L。这些电压在模拟放大器的作用下会变成模拟电压G,后者进入到模数转换器后,最终变成了数字信号。
Tips: 辐射通量与光源的光亮度正相关,而光亮度是表示发光面明亮程度的,指发光表面在指定方向的发光强度与垂直且指定方向的发光面的面积之比,单位是坎德拉/平方米(见27. HDR - 高动态范围成像)
如上图所示,这里面有3处都会引入噪声,首先是在传感器部分会有光子噪声和暗噪声,接着在模拟放大器部分会产生读出噪声,最后在模数转换器部分会有所谓的ADC噪声。你可能会问这些噪声是什么意思,它们又是如何产生的。不着急,我们一个个的来介绍。
二. 图像生成过程中的噪声
2.1 光子噪声
在对光电效应和传感器特性不了解的人看来,当传感器像素受到恒定亮度的光源照射时,每个单位时间接收到的光子的数量是恒定的,因此其通过光电效应激发出的电子也是恒定的。
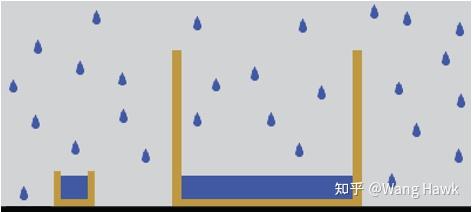
然而,像素接受到光子,就像下雨天你站在室外淋雨一样,滴到你身上的雨滴的数量以及像素捕获到的光子数量都是随机量。
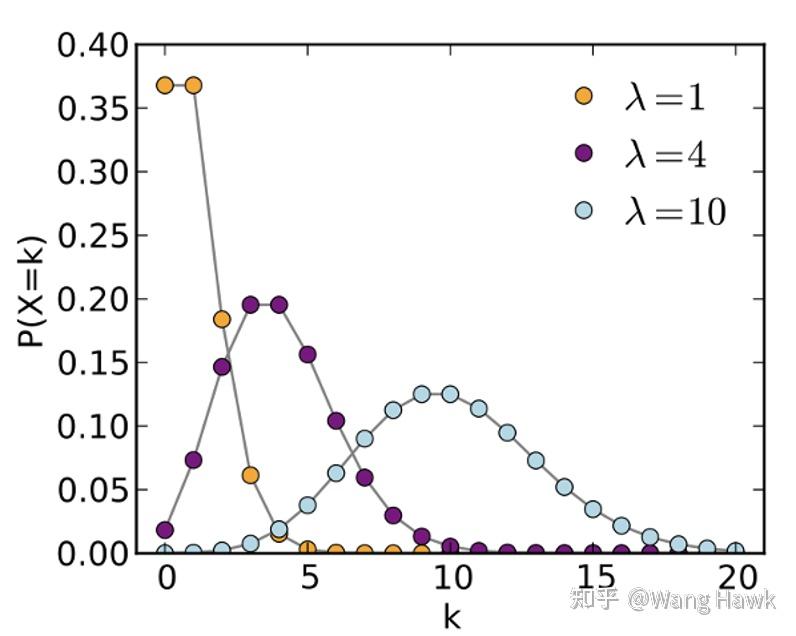
这种随机量围绕着某个均值波动,并符合泊松分布。传感器像素在单位时间接受的光子数量的这种波动性在图像上表现为可见的噪声,也因此它被称为光子散粒噪声,或泊松噪声。
泊松分布随机量有一个有趣的特点,即其平均值和方差是一致的,下面是这种随机量在不同的均值情况下的概率函数示意图,我们可以看到当它的均值 \lambda 越大时,其方差越大,表现为曲线覆盖宽度越宽。
回到光子噪声,我们可以认为单个像素在曝光期间接收的光子平均数量与曝光时间及光辐射通量 \phi 成正比,因此可以表示为下面的公式,其中 \alpha 是一个比例常数, t是曝光时间
光子噪声有两个典型的特点:
- 曝光时间越长,或者场景辐照度越强,平均来说捕获到的光子数量总体越大,其波动也越大,即光子噪声绝对值越大
- 光子数量越多,噪声绝对值越大,但在图像中反而越不明显。这一点在我们后面讲信噪比时还会再仔细说明,但现在可以通过下图得到一个直观的印象,我们可以看到,当画面较暗时单个像素捕获的光子平均数量较少,其波动也较少。随着图像变亮,光子噪声增加变得明显。但当图像继续变亮时,虽然光子噪声的幅值变大了,但从肉眼上看却变得不明显了。你现在可以在心中留一个问题,我们稍后来看看怎么回事。

2.2 暗噪声
我们都知道光电效应会导致传感器激发出光电子,然而传感器即便在没有接受到光子时,因为温度的影响也会释放出电子。在曝光时间内,这种电子的数量也是一个符合泊松分布的随机量,我们可以将其表示为下面的公式,其中t是曝光时间,D是当前温度下单位时间内的热电子的数量):
这个随机量也会导致图像上的噪声,我们称其为热噪声。它有以下的特点:
- 它与温度成指数关系,温度每升高6摄氏度,暗噪声的均值扩大一倍
- 它与曝光时间成线性关系,曝光时间越长,暗噪声越强。
在天文观测一类的长曝光应用中,暗噪声影响特别大。如果要消除暗噪声,最基础的方法是
- 降低传感器温度,比如超低温环境下放置传感器(例如太空中)
- 或者控制曝光时间
- 提前测量出暗噪声图像,并在最终图像中减去暗噪声图像,这一点我们稍后来看看如何做到
由于光子噪声和暗噪声的存在,传感器像素在进入放大器之前的输出电压L也是一个随机量。由于两个泊松分布之和也是泊松分布,且其均值是两个泊松分布的均值之和,因此L可以表示为:
2.3 读出噪声和ADC噪声
如前所述,像素在光子和暗电流的影响下释放出电子,曝光时间内累积的电子被转换为与其数量成比例的电压。然后该电压被放大成与相机中设置的ISO增益成比例的量,并在模数转换器(ADC)中数字化。
代表所有像素的光子计数的数字信号构成图像的原始数据(原始单元有时被称为模数单元ADU,或数据号DN)。我们将这个数字称为像素的原始值。在理想情况下,记录在原始数据中的数字应该与光子计数成正比。在现实世界中,原始数字并不精确地反映光子计数。信号处理链中的每个电子电路组件--从传感器读出、ISO增益到ADC数字化--都会受到电压波动的影响,导致原始值偏离与光子计数成正比的理想值。由信号处理电子设备引起的原始值波动构成了传感器的读取噪声和ADC噪声,其中ADC噪声还包括了因为从连续的电压值量化为离散的整数值的过程中的量化误差。
三. 包含了噪声信息的图像生成模型
考虑到前一节讲的各种噪声的存在,我们将放大器的输出电压G表示为下面的公式,其中 n_{read} 是读出噪声,而g则是一个和ISO相关的增益比例。正如你所看到的,放大器会同时放大原始电压L,以及读出噪声。
而经过ADC后的输出数字信号可以表示为:
也就是说
这里面读出噪声和ADC噪声都符合高斯分布,而原始电压则符合泊松分布:
这个数字信号I的均值和方差也很容易可以计算出来:
这里面,由于读出噪声和ADC噪声都符合高斯分布,我们还可以将整个成像过程简化为下面的"仿射噪声模型":
其中
被称为加性噪声,它是两个高斯噪声之和,它也是高斯噪声,因此有
我将前述所有的信息总结到下面图中:
我们从这个模型中可以观察到下面的信息:
- 因为暗噪声的存在,像素的原始值并不绝对反映场景的亮度
- 拍摄多幅图像并取均值的方法可以消除读出噪声和ADC噪声,但无法去掉暗噪声
- 为了去除暗噪声,需要专门测量出暗噪声,并从最终信号中减去
关于噪声还能看到:
- 场景很亮时,光子噪声起主导作用
- 场景很暗时,加性噪声起主导作用
- 最重要的是,由于光子噪声和输入信号本身绑定在一起,所以无法消除
- 低ISO值时,ADC噪声会更突出,而高ISO值时,光子噪声和读出噪声更突出
- 曝光时间越长,暗噪声影响越大
四. 信噪比
现在我们有了新的问题,由于光子噪声和图像的曝光时间及光辐射正相关,那岂不是意味着图像越亮时,噪声越大?那为何我们在下图中看到的不是这样的呢?
这就牵涉到一个重要的概念——信噪比。
我们知道,信号的方差反映了它的噪声的绝对大小(的平方)
而信噪比则反映了噪声相比信号的相对大小,当噪声减小时方差变小,而信噪比减大
现在回到传感器信号,如果我们不考虑暗噪声的话,前面讲的成像模型的噪声和信噪比可以表示为:
观察一下信噪比公式,我们会发现如果曝光时间t很大,或者场景很亮时,我们可以忽略掉加性噪声部分,此时
也就是说,这种情况下像素值越大,信噪比也越大,噪声在图像中看起来越不明显——这就回答了我们刚刚的疑问。
反过来讲,如果曝光时间t很小,或者场景很暗时,光噪可以忽略,加性噪声占主导,此时
可以看到,如果图像亮度保持不变(即SNR的分子不变时),ISO越大,g越大,SNR越低,噪声越明显——这就回答了我们本文开始的问题,为什么高ISO值通常有更大的噪声呢,因为读出噪声被放大了:
那么,在我们对下面的RAW图像进行色调映射,拉伸暗处细节时,噪声加强也是很自然的了,因为此时暗处噪声的绝对值被放大了,而暗处几乎没有捕获到有效的信号:
五. 各种噪声的标定
如果我们能提前测量,或者标定出上述成像模型中的各种噪声,就有机会在最终图像中消除它们,从而得到干净的图像。 这一节我们看看如何做到这点。
首先看看,系统噪声模型中的哪些参数是我们需要测量的
从上图可见,暗电流D, 读出噪声 \sigma_{read} , ADC噪声 \sigma_{ADC} , 以及增益尺度k,都是我们需要知道的。那么,如何获取这些量呢?
首先我们看看如何标定暗噪声。
5.1 暗噪声
根据仿射噪声模型,加性噪声的均值为0
因此如果我们把相机镜头遮挡住,并在这个状态下拍摄大量的图像,再对这些图像取均值,相当于在令 \phi =0,于是这个均值图像相当于:
虽然此刻我们并不知道g的具体值(它是一个跟ISO成正比的常数),但我们由此就知道了在当前ISO设定下,一定曝光时间的暗帧。
这意味着什么?意味着我们不必求出暗电流D的具体值,只需要在同等曝光时间和ISO设定的图像中减去这个暗帧,就可以消除图像中的暗噪声。为了消除在不同的ISO设定下的暗噪声,我们需要做的就是在相机的不同ISO设置下分别标定出当前的暗帧即可。由于曝光时间可以任意设置,我们很难针对每个不同的曝光时间去标定当前的暗帧。 但可以用暗噪声大小与曝光时长成正比的原理,来进行一定的比例补偿即可。
这样,消除掉暗噪声的相机噪声模型就变成了这样
5.2 加性噪声
接下来的问题就是如何标定加性噪声了。
观察一下此时的图像噪声式子:
这意味着:
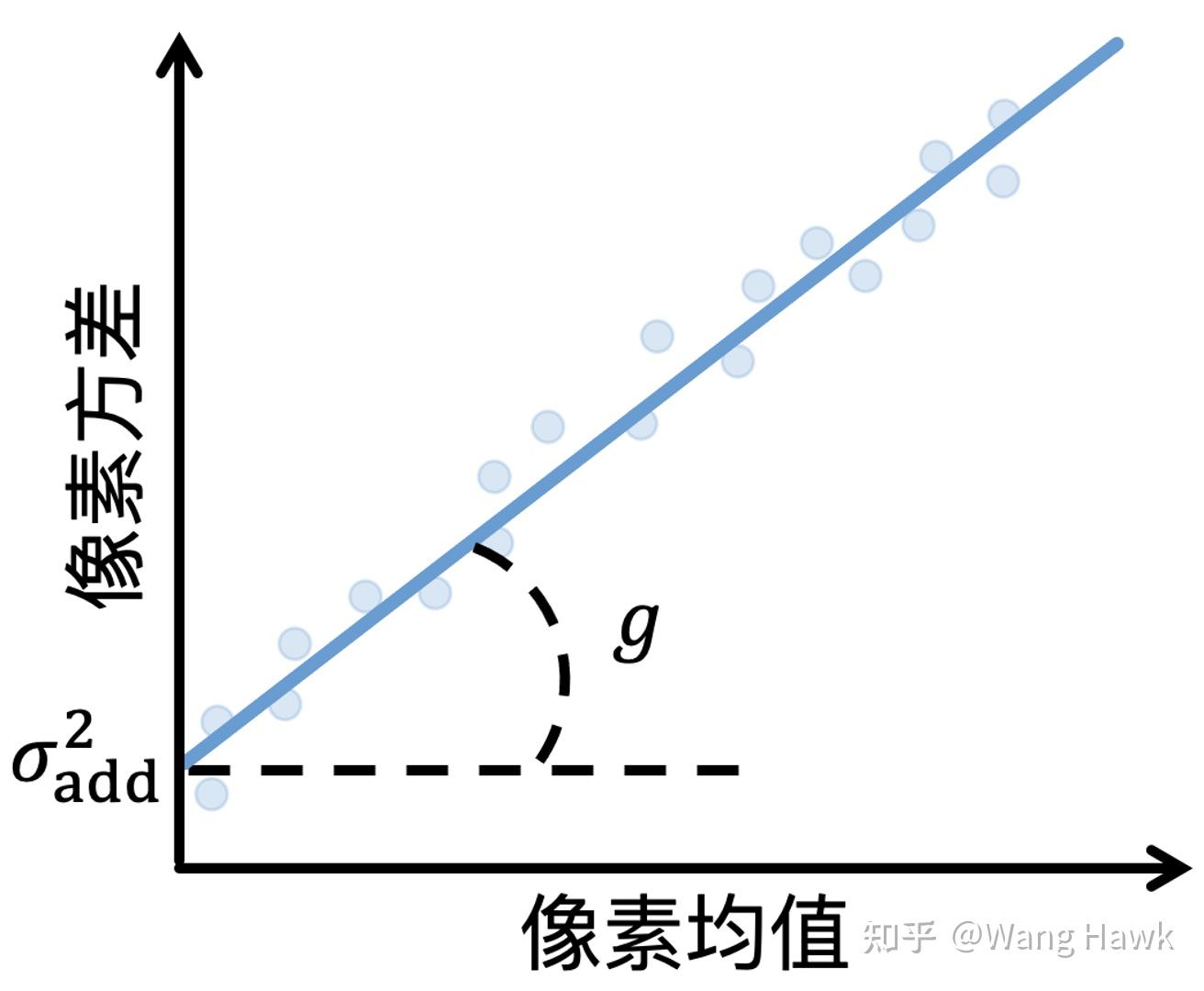
可以看到图像像素的方差与像素的均值呈现出来了一种线性关系。于是,我们可以在特定的增益g下,拍摄大量的灰阶图像,如下图所示。
然后对每张图像,我们首先减去当前的暗帧(需要按照曝光时长进行补偿),然后求取每个像素的均值的方差。此时如果我们把大量像素的均值和方差画在下面这张图上,可以看到它们几乎形成了一条直线,并且增益g是这条直线的斜率,而方差 \sigma_{add}^2 则是这条直线的截距。通过采样大量不同均值的像素点的信息,可以很容易的拟合出这条直线,并求得g和对应的加性噪声方差 \sigma_{add}^2 (这也是为何要用上面的灰阶图卡的原因)
你可能会问,我们有没有办法分离读出噪声和ADC噪声呢?当然是有办法的,根据下式
因此,我们可以在不同的ISO设置(也即是不同的g)下,多重复几次上述实验,即可获得足够的数据,拟合出 \sigma_{read}^2 以及 \sigma_{ADC}^2
六. 总结
今天这篇文章,我介绍了一个简化的相机成像的噪声模型,其中包括了
- 暗噪声
- 光子噪声
- 读出噪声
- ADC噪声
我们看到了信噪比是如何计算的,这些噪声又是如何影响信噪比的,对实际图像的影响又是如何的。我们还看得,通过简单的方式,就可以提前标定出暗噪声、读出噪声以及ADC噪声。
在这里,我必须强调一下,前面描述的过程的前提假设是每个像素的噪声特性以及对原始光信号的响应都是一致的。 然而,事实上传感器中各个像素因为生产制造、材质本身的非均匀等等各方面原因,会导致传感器各个位置上的噪声参数都是不同的。也因此,上面介绍的噪声模型只是一种近似,如果要精确的标定成像系统的各种噪声,还需要更多的理解噪声模型。在这方面,有更多的资料做了更加准确和深入的讲解,我也希望之后能够用比较清晰易懂的文字再加以详解。先给出一些重要的参考资料:
七. 参考资料
本文基本上是对如下资料的中文讲解,如果有讲得不清楚的地方,也是我自己的理解不足,与原课程老师无关。
CMU 2020 Fall Computational Photography Course 15-463, Lecture 7
在这个过程中,还参考了前面说的两份资料:
Noise, Dynamic Range and Bit Depth in Digital SLRs
今天内容比较多,也容易引起争论,欢迎你的留言讨论。在下一篇文章中,我会讲解该噪声模型在HDR融合中的应用,看看有没有办法融合LDR图像在保持高对比度的情况下,还能获得更好的去噪效果,敬请期待。
我的这个专栏会全面的讲解计算摄影学相关的知识,但无论之后你看到的内容多么新奇,计算摄影学最最基础的部分却首先是”获取图像的过程“。虽然我在专栏里面已经做了一些讲解了,但此前还是缺乏以视频形式对”成像"这一基础过程的传道答疑解惑。现在,我酝酿已久的构建在国际顶尖大学相关课程基础上的计算摄影学系列视频课程总算落地了。第一季讲解的就是刚才我说的“成像”这个过程,除了我在专栏中提到的一些内容,我特意增加了一些重要的与相机成像的知识和实践作业。在这个课程中,你有机会练习制作小孔相机并尝试获取到最佳的成像,然后用它真实地拍摄你周围的环境。有机会学习如何用光线追踪法准确的绘制光线透过传统凸透镜和凹透镜、甚至复杂的透镜组的走向,还能学会用成像理论分析DollyZoom(推拉镜头)这样的电影特效的原理。你还可以学会量化的分析镜头的景深,学会如何计算镜头的等效焦距,为选用合适的镜头和相机组合准确成像打下坚实的基础。你还将完成一个较为系统的大作业,学会如何用单反获取到RAW图像,并写出完整的代码将RAW图像转换为我们肉眼可见的图像。如果你对这个课程感兴趣的话,可以点击下面的链接了解详情,希望对你有帮助:
本文同步发表在我的微信公众号和知乎专栏“计算摄影学”,欢迎扫码关注,转载请注明作者和来源


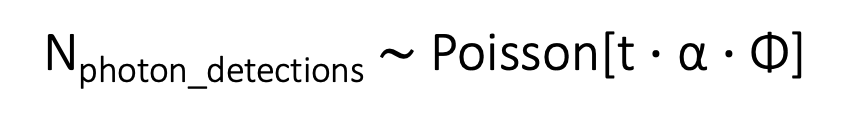
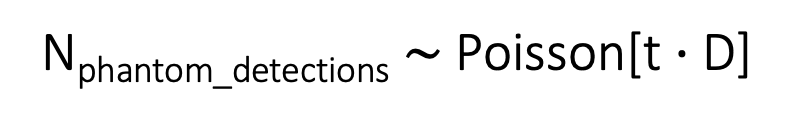
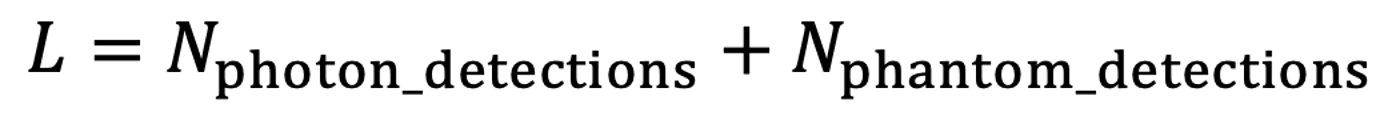
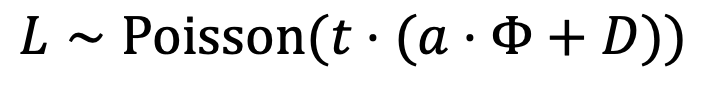
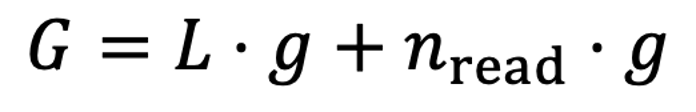
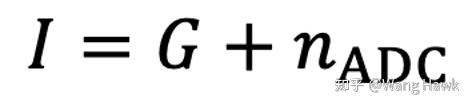
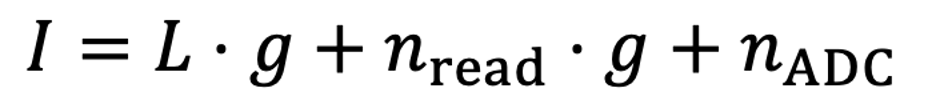
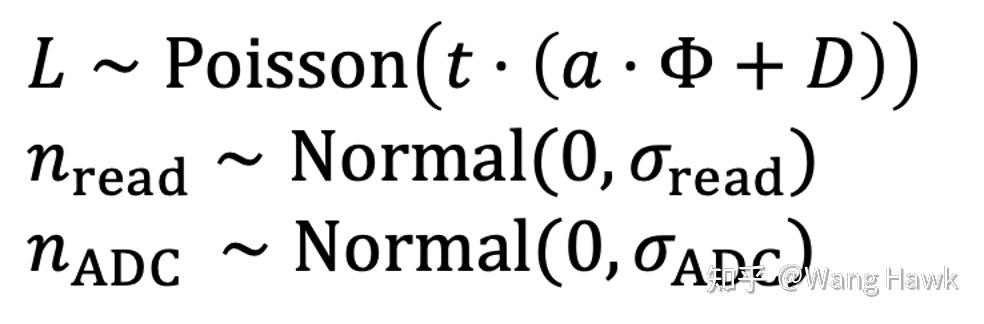
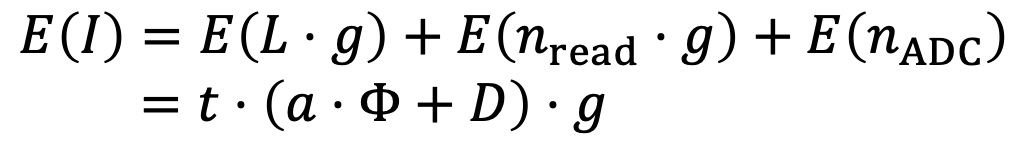
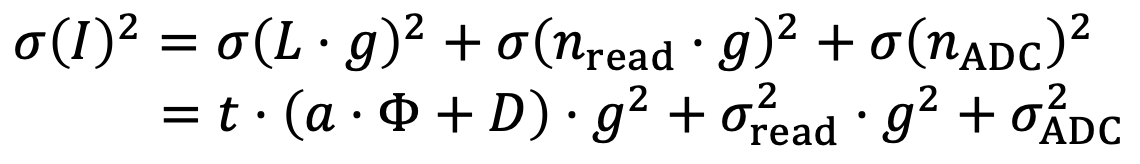
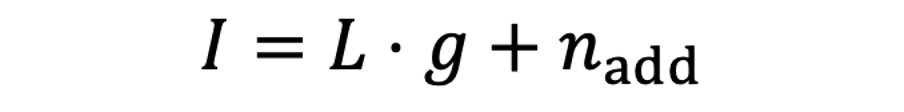
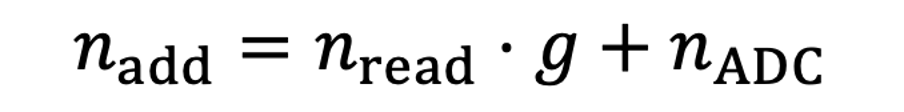
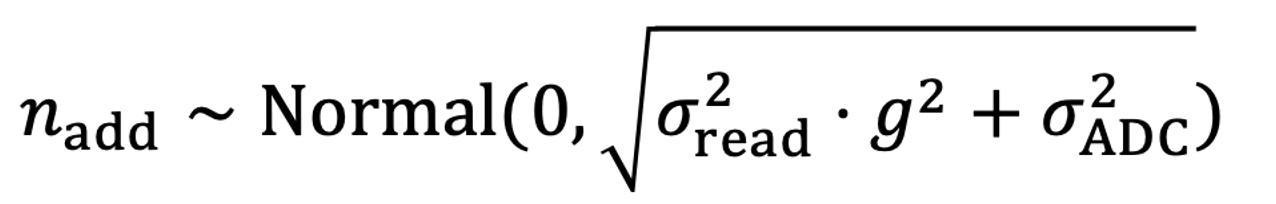
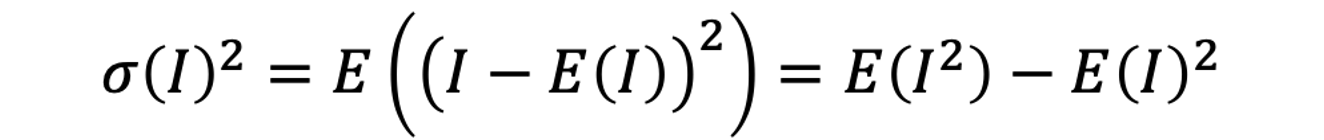
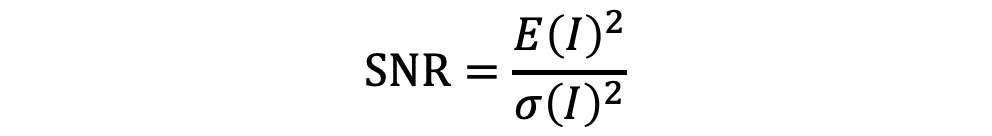
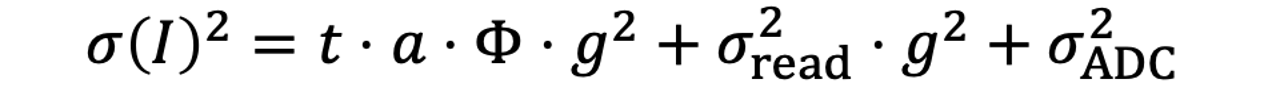
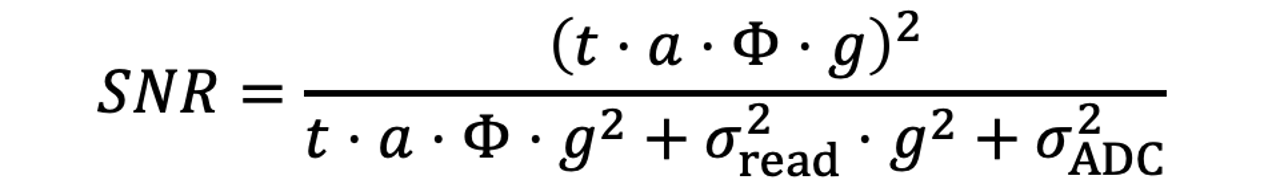
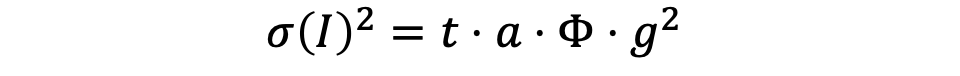
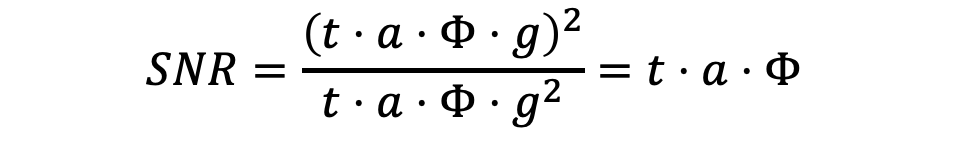
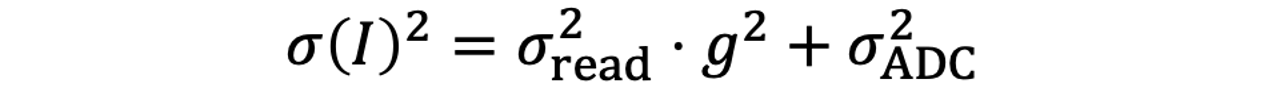
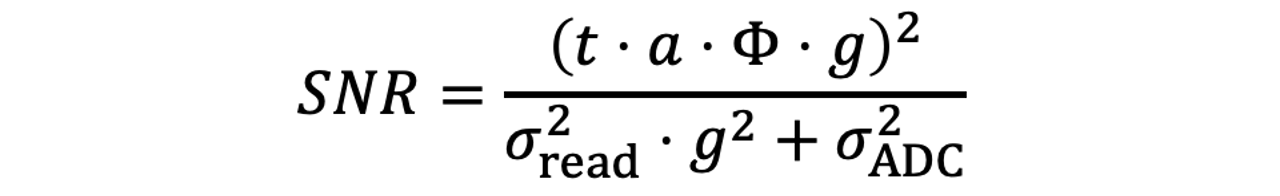


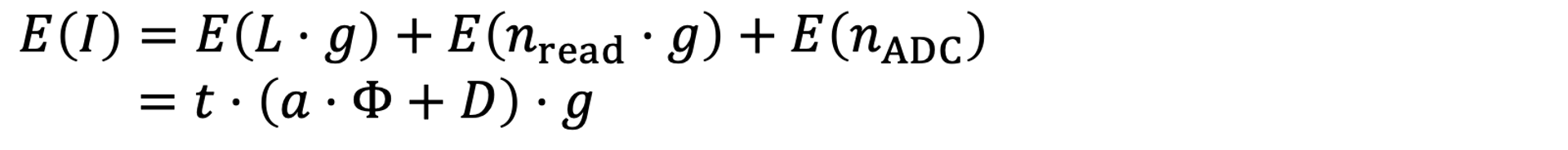
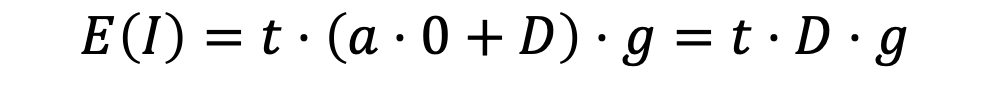
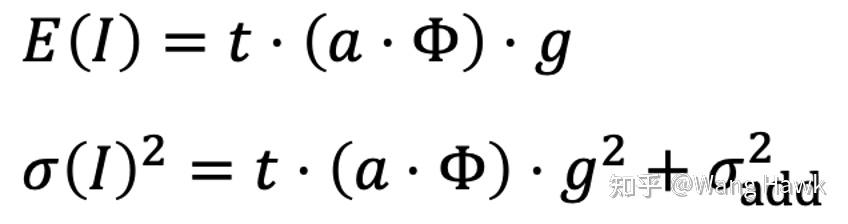
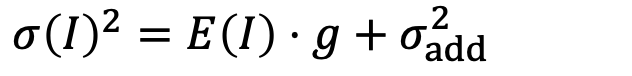

感觉这已经是读噪声的终极解决方案了
谢谢博主,一直以来没搞懂的相机噪声终于在看完这一篇博文后够清楚啦![[酷]](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEIAAABDCAYAAAAoCNNNAAAKEElEQVR4nO1bbWwUxxl+ZuH8UTjubGIO4w/C2hy2XFOVGErkCBCI4AgpSglEsVPR0sQlQlRqSx2kJvyCVsWI/Iiqa2gSUVXpmaZJmoRGMUWOIAppGgxqghCOw11SY6BA4rvDEM4f7PTH3ezN7s7e7t7t0VbyI61mdmbunXeefd/ZuZ13gClMgQe50x0OheD3lqEcFCsoUC1QaJgAFylBpKwd0TulV8GJGArB7/XjIQqsALBSkojs5PeKQo8AuCQBPf4OHC2MlgUkIh7GWgXYIUlknVsyFYVGARwnBHvcthbXiYiF8QMK7Mr25It9dQCAkqI5QLEXmF6SqphMIjkaAQCMJSJZ+1EUetBNQlwjIm0Bz4sIKPbVoeQbNVAqvwnJNw+YXmxP6OhV0MRljF06YUqMW4TkTcRQCP6ZfhwSuYCvclVq8LMX5NsNAIAOfywkRVFolAC7yzrw+1xl50WEmRX47n4QWLDc/pN3COWrzzEeeUdEyMEbcfysdhviTmXmTMRIGM9IEtnNlxX76lCy5PGCEaAHHf4Y18/9QVOmKDRKCNY6dZWciBCRMKtxM0j1t1I3k2OpdHpxKs+nrN4qz98zebxMhlsJIPIeEtf+rhblQoZjIkQk+JbvBEp95srmCzvyPv8QiS/eUm+dkuGICD0Jxb46lCz+3h1zBSvQfw9oXMUJGZLdToQksPmAPS2zlMGqndNUJ5fMbYB3yfbM4CQiU4qjQyH4rcZni4hYD2QQ7GD3xb46lDRuTClgZ9B8O1G9PhW5gr6cl8vKJ8cg+eZhVuPmzAAlIs/041mrMdoiglIclQhRWS2qewDwlIgbW/mynbmDb2OWz9Ke3LUg9QpPQ5LIlpEwnsnWpSURaZdQ1wneJdshzZgtbjyRtBJnD7wcs3y2+4kkUPNtdSkPACDYkc1Fsk6WsR7IhBB11eKrXAXM/475Dzwl7pAhkqMvs+orXZ/4cK9apCj0YHkHfihqntUiKNWZEyOBuYU+ZYqZ1dtNRXLMSLCQoZsvtsTDWCsaqykRsR7IkkS2sHve5zQmyKdW9XZTPSHZXMJCF+Kr1LiIgsykz8OUCIM1zG00a+o+3Jpr0iie16rmJYmsE80V2VxjJctorOH/EHqrmOnHdkMb3f3TQTmwZzB6xVVF1retxlvPNUEqmgEAUMZvQiqagX2/fBUv9o3C7f6CcgB9oVZUNwQz/Y0MqUtwhdJ4eTvK+N+oRDQ3Nz955syZ37qqEYfuznrs6HpAJWN4YBA1ba8XqjsE5QDO9T6iKRs9/ZvMjULv57+Bqq4xMDCwpmBaAXixbzTV//hNKOM38cGJc0oh+xuMXsGl6EVNmW7SFK8DPB7PnwFQ/RWUAzQoBwzlhb7c6nN922p6oXcDvT34Y0rfX0fjhwiNHyJ0JIxefvyqRUxMTPxTT05QDmBhsAkLg01C8gqF9W2rsTDYhKAcyFvW273voqbtdezf9w6od26mgmgtIuuCihHw2eDZvBWyi/Vtq9W8m5PoUy+cR8N3e/G7vpR7SIT4Yz1Q/zqoRDQ3N39VSIW6O+txoXeDen10oMXQhreAfMkPygH8aVejwsscjF7BUy+cx7JfzMFg4h4QCnXS4InoFyn0du+7eSnEY55cpV4ty43uxltgvuQvDDZh08ZlUl+oVfNQgRQhy7b2gwJVrEwl4tf3hc8DmXmBKeQWVrX4QW5dVy/WF4PbFriyZghAivzDe2twoXeDpo+gHAC/96oSUbsNcY/H8yo/Mbrlo0E5gJblTaClswBATZ9Y41XrGdyywPaHFwOASnpVpReH99bgowMt6FpRhJd31mjaaybLhoaGPrcVAjImz5RiafvDiwtigUE5gKpKr7CuuTaOp7dNIOg7pSnXEMHmCTddIigH8PxPxN9Dqiq9qlW4MS8w9IVarRvpoCEiHA73b156WXHztbX7sXLF7OkAKatwk4TuznpTa8gGwzpibeO5L7o7611TatPGZWofZOKWoU1VpRd9oVZXFk/r21bj59tbTfvSl0nAP7i8Acd/tCZieAc7RXdnPbq2LtEoQD2lIBO3NBcAVN81PW8yujvrcXhvjaYv1je7qKfUdFddREQUANY1DUgv76xB14oiRwoF5UBqZt66RB04rxCvJF/PyHBqjXx/+r5EpPC4HsdJljd8vI2HsRYS+Ru799VvwvCXk+h57RPTbwdBOYAn1nixqsWPpffImgEyiMpEoJ5SXLw8ig9OnFN2/XFEAoyvcX1/tuUnE0gMp4amKDRa3pFZWRqIGArBP6ucxNi97+4H/2e29PJF8tpp1TX0X7QNrlG7DfF0AFfqxzHBq1S00eJk0zdbW0HdK2+eUfYdOI3hLyedy+PAzw8EeI+vM/v3+b6hI7NtO/1OlGgbUL9Nx23RGep123qvvHlG6T8eka59OoSe1z4RyxPpo29z85pG9dE43rAkghCEWX4sEQEmua/K+o54xfWxDaKUH3CWdidPRbHvpbPoPx5RdZw/16MI+xfJ1OmV/PqC2r2i0CP6qJrpIiLK2hEdCdMjLC4qORpBSZnJxxmLvcnh+DQ896u/omJRLebP9SgLqmdIAFA5vxbVM5OpiLrJJIZvzMDlf6X+KB3rj+Pap0MaORWLavHIulrjg7OzT5pMaNxCAvbrxZhu+RneHjl+0t/30lnDoJyiYlEtur5flwlDdIhk7Cw/SWreFgymX6j8HTiaDvBUhalgriJKdflVLZahCaaoWFSLTY8tRtfjnDVq3DSLHpwOuklSE+3DlZvDYBUV92YCRCczZg0gaxkz+2P9KbfMZiG8Cy1tmi2Wy2BDj+RoxNIaLIkAgJEwevkYSl/1/cZGeiX197fHU+m0Ik3Z8K3MHkt1aUxbbyVXRIwOPAkAQBW6xSwW05KIWA9kCpxigSLFvjqUeIWkOgcjCDCS4ILsxOVj6m22kADARqBIWTuioJlZdiwRUeOl88a0oszlMnQkRAnBnmztbYUOlXdgD7/a1JDBnurtcW3eLLWTZ7AjT/B79n+CG+STVpF1tqPqbsTxKP8WEZIxrUirnOjeKi8YmCE1kwutJQCAotBdds55OIqzjPVAphRH+ZgqFnlfcPCDF2FyTBN9C6RIKO/I7hIMjiNvTckomvPf+ZeaXkHmQwKQYyy2iAwgvc4QxV/nE4/NIJIFIDl+VRSl74gEII/o/PQ5jWf5OCuAsw7AHhlm7Szqk19fMBJAaZxQ/DSXcxt5H1wRBakz+Cru1RbkEqyu+43IAoDcjycwuHKUKe0qIbODbBoryQHJ8asAxOe8FErjoNjv1BX0cPVwm5ODbQCE5LBBA3f2gFtBjjumCXnUzaOODMwCCEHYzSOPBT0Am3aZDgBbnB585ZEe/F8koOd6HCdzObNlhTt2JHooBP8sP5amg7juSxcvBEE5+0PHrVw/A3AJQNTtJz+FKUxhClPIA/8Bhx/OfZ1hR6YAAAAASUVORK5CYII=)
图像信噪比计算应该是均值/标准差吧,好像不是均值平方/方差
噪声参数在标定的时候,采集到的图片的应该不能归一化吧
这个不需要标定,可以从分布模型直接计算得到
这个就是黑电平(Black Level)的标定
作者一个人![[好奇]](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEIAAABCCAYAAADjVADoAAANVUlEQVR4nO1be2wcRx3+Zvfs9d7D5+bOlzjFj+BHG6d2mwDFRonixiEtUYG2gFohNZLrvlvxkAj80ZRKffAHRdCCKxSSUpGAKEoRSVvUBwlxaFQHlZbUbkpqJ+RiO3bss0Pse3l9tzv8sZ692b3d89m+IP7wJ512dh7fzHz7m9/Mzs4By1jGMpaxjGXkC8Lf7OsQQn0Dwq0AvkQIVlGKiwDeePZ4+teFrnhfhxBqa9FKAaD7hDC94yVtvNB1LASGEPs6hFDvgPABIeRqayZK6YXmem3DYhq7r0MItX5Gayr14TZRQDkR0CKKQrVdXlXVzmsqzmkUH01HcbDnfaHvfyUQYY11EiGTkR7/8TvpTfkSD3ShvawUuzRN3CyVUDJ/CXukZrXu1Cz57ep76YuL5cgHBAB2bnTdA0IyFVHaef9d6fO/etlVTYEnmUD335naWv8ojjiR7esQQl/aot2nqeJTuTrv8jWgRA6Y4maSkwCAdLTftoyqauc1DXuSCfyh6gGcyb+L+YEAwPc3ud6hIBsBAJR28j7hextdzxFCvq0n0ed/cjz9HTuigS60r7gKL9qZvb9yG7RgHYTAmrwapU2eA4mOIzHWmyUME6T8bjyTZx/zggsANIo1ZO75NdVrr+N4JgMBenMRDO5GnSxjT1Gx0MbHe0OtIFevNzovLKBRQmANEFgDT83nASUG9ZO3ERvvAQCIolAtinh68nfaffEYthbKOgQAEAjOAbpT5J3Tvg4hRIEn2b1VlIEutHu8OMyL4A21wr/pCYjNd+RtATkheSE23wH/pifgr9xmRIuiUC1JYn9kPx5beiXcrDHQhXbeSw90oX33y67fMP9gnTki+/FYUZHwNE/mW/9wYTqfC0oM8ZO/Nw2ZVErbdXkKJ6QinF+shdg6NKvzpJRe+Nbd6TZWiVUEb6gV4jXbAMkLKDHzdSmwcimxTFq4B1NDb+vZZgiVSihRZgh1FamDVMOJRAK7FiKKrRDf2+ga5i0hlwj+ym1ATWs2ibXhi4WVh7uPn/w94pEBalfMVaQOLsSpZvmwnRtd91iHAxNhoAvteYkAZDd+IVc+bBWTu09E43rWEkoCVS3EU15P2LSdTolVmio+Nfk7hAd3o86+kRnM58xfYT5hcDfqVlwFY7jYiuDUMdb4fK/WsB0nB2WGUCFYD7luK3zrH0agqsWw9HRKrPJ4cXg+MbKEaKrXXgelr4DSV5rrtR+xeFnGHrZG8IZa7S0hV8eWChvOFaEqIxz5YD9NnjkMosRArl6P8g13E1Ky2rAOSRL7c4mR19J3ZC/pdHvJXnbv3/REVp5LwxMYDU9jbMys7cqVGipqSrHiU8F8qlowX+SdvaAzI4afkEooYQs4AEieOWz4EVeROui09sgSYu4N9AUAaKrXHmlr0Uo9Xhxm1uBb/zAEb7mRX4tF0P1WHMlYMmfHZK+Mtps9prJ2WBRfuAeRoVMmQQJVLYRcvR5Athh/PizcaH2ZE60V1PvEN0HILSCkcXySrGlr1YIul3AHMDdNrm428l4ansCJY5lGy14ZpZ9uxcqGz6Osch0ETwCYiSA9m0Z6No0z/0ogGCSQS922nVs0X9U1kAOVkAUXSU4N652fGoanrJpA8qBoxaeRnBghSEehaYK/bo0m/+Qg3uDrzrKInRtdB0DI1/VEevwHD6Yr7ayBf3KyV8bK5lsRqN2AYndpVgdH+7ox1vu60cHW9vKsoXJpeAIn/x5bMh8/pfJWQZQYIh/sNyxGUdQGfojYOctHCOhxAnp85/3pN5kILl8DBG85tFgEAEwirNnyECqa2mwbDQAVTW1ovP2HkL0yAODk32MGD7vyIiyFj4cQrDfCVPKaZhNZxh4+b05nGdmHo+w9orRxB6jkheAtx6XhCfQc0Suu+cI3EAn34cx7rwIA1rV3YlXD5+CvqM3imxo9i49f/alerlbC2ht8Beeb/Ochw1cEWx/K6h+fzluFy0mEwd2oYyK4fA2gc/O3FotgNBwFoI/hngPPoL+3zyjX3/sd+ANBfPPpQ1mN91fUwrP6WsRHTmNsTMDaK8DHOsmmTqLEQCWvcV0RqsLk4Ihenxt3AvrK03FB5RLJZhb2lNWY0sJnFQDAvz/50NRohqnJCRz55YO2vNWf3Q4Aplmh0Hy5wA+XeFQ0VsmOQhRL9IssTH2rbPOMXRh1rNCuQwAg+zPT5+XLZsstBB+zBDozQollQceswlNeTwBAdoMOdKEdyCFEKkWuY2HKLWv5xk9NTjg2HABmE9M5068EH1ttJhMgiaETADICsDBv4Z4SUgPkEEJ2k3WA7h94lJVlXvb8AefVoj8QtPX6ySmzdy80HzN92Q06cX4AiaETwGwCvHVQSedJJkCY5dsKYbcmZ0REiRnT1g03brZmM7Blxy7b+MTEkBEuK6MF56OSF+XXfY0kEyBMjMhHf6QkejFTqFhf0MluGE/BVgglBWMDtkQOwDrWVq7UdCKvjNu/+5zpSfoDQWzvfAzXbL7LtuFjva8D0Kc7xltIPqLEgGI3qq83XBySCRBViWaVTSZAKMVKIMf0yTCTnIQburmxhjeuJQif1T21MB3BQy9+hNG+briDlZD95Y4LodG+bsO7N67N+IZC8+n+YBUCVS1k+PQJ9uRzrpnm3Vy2fn9gqKmVAADxkdPofe0XCNRugL+i1rHRnxx7GeF3D5jKXik+9sDYt5JkAkSUfKY8yYRZmAVZBA/9CUgIn1UQHzmNj//0ZNb7wWxiGpNnP0Ak3If4yGkAuvk3rs3eXSs0H5DZwQIsS4DZhBEkBGOOQkhFOO+ojEPjk7Ekwu8eQPjdA4bzsy5yamolNNbGAdi/fRaab26VSYyhMScAUTLTsKohAjgMje4TQvaEPZvIKMmFG2uT2L5NM5lnMpY0NVr2yrhxQ8oYxxMj0QxPAfjs2keiFw3z95TX6yIUZwumpshJwMEidrykjY9tFqlUQkk62g/Mzu1BFLszlbHw3LWxNonGWmBiQjVxBYMigDgAEUdefQ9vv5X5HtHQ3ISvfnnNXB7kz1dMgVluK4Urx8Lxscy3KMPPzbU9fjlspMVnaBjI4SwFQT2WFcmNLdPT5Bu62odgUDR+DEfePGWIwKbH/t4+PPvMqyZTNQk91/EsPru6LWHePwil3Ef+Yrcpred9oQ/I4Sw1io8AtAH6mGKrsXlhEYYhPKqb+rabG9B+yzpMTKg49No51FQo9twOPPmAKNNIXNLfMN0rVmfxsjSpRDu14yU6DuSwiOkoDrIwb0qLRU2F/obJBAkGRXR21KH9lnVL5raCb6/b5zGladMXjLAg0qNG2Ims/lEcUWYIBTJnFpgJL+Z6/WevBaAPhx89/Y4x9pfC6XTlTd+6hXBpfNAI8w8794KKqC+wIFOSDRPTuJ4nHgDKfXHsfOwrAPS3TN43WMvy94upix8W1nwsDdAfdl5C8IrFxnuMscyIrZXwvsTOr3z4j9NGuKG5yeCwcvL3ufjt4iNDp4z4XMNC9qhdfFpOIeofxZHUrNZtR8SLwBphjePDkajHmDW23dyAe78ZyuqEEyd/tea3luOfuHtls8l6nIbFvEIAwOVpGNtZ7NQKa5C1EU4WQZRpHHrtnCHC1psqTXVYn77TMLFL46+8NQSr67PS+dnCehZsXiGsVmGdQZzGqV0aAFxfp8epShSHjw7h8NGhrDx8OSqVmizRysnEVpWoyRqsTpIXiWr4mbXOeV+6ACCZxH2aRvrZSlOVA7C+zc2HmgoF/b3Asy9chD+QNm3L3fSFMkc+okznrEubvgBR8pnM3rp2iAydMllDxT3ZRxXzOuNV9QDOCKL6OLuPjfeA3+iwbnrY3W+9qRLbbta3/ZgIDc1N2PnIqqyO2m2iONUnSj7EL4dN1lBemVmb8CIAQCpFb7Pr44IOgk7sx8uuIuFOdu8Ntdp2go+zu59JTqLEwar4/Cxs5bDmO//hX4z4T13bYsRbRfD41F1OJ2iyPgLnwnVlwt+qVtPtRUUkBACz8WEUlYQguCSoShSCSzKF+Y7w98UlZaDqLASXZHSKT7d21MrJ1zM5egapZMZCij0ypiIXMBH+0BxfrN27qgPPO/VtwUeDB3ejjj8mAGQsw+4J5rKQ+cJOFsGGRmy8B8oModbdJh5SiXYqlqDfznViGFjYOVAAur+Ix7BVVTVj8yY23oP45XBW43nY3bN8TmWsYHlZnYB+MMQur8erdhcXa/dW3EOvm08EYBEWwbCvQwht36L9nPcZ7Iy1nSB2TzjX1a4MoG8d8mcskwl6KpWitykpVLOPNWmVHlvoectFC8Fgd/AUmDtnVUBYBQAARdG63uoWnirEXxmWLARg7zcY7E7iLwT8apZBVbXzl/6DznxMPl8URAiGkb2kU5Lp405/TOE/Hzr9TQFw/quCMkOoIKqPv/FXYU+h/9BSUCEYRvaSTiLgu+z76VJxJQVguCJCMAzuRp3sxp2g2Gr9G8N8SCboKUGkR6ejOFjIIeCEKyqEFewsQpkfLZqGVaKAckD/tiAIuJhSyMW0So/9P/zZbRnLWMYylrEMZ/wXencHIEogJOMAAAAASUVORK5CYII=)