解读PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing

109 人赞同了该文章

0. Sources：

原文：Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: A randomized correspondence algorithm for structural image editing[J]. ACM Trans. Graph., 2009, 28(3): 24.

【PDF Access】【Code Access (matlab)】【Code Access (cpp)】

1. 要点速览

要解决的问题：寻找最近邻匹配是一项非常重要的任务，cv领域很多任务都会用到它，如立体匹配、纹理合成、图像修复、non-local means去噪等等。而之前的算法都太慢了——最原始的暴力匹配速度极慢，基本是没人用的，后来比较经典的加速策略例如KD-tree搜索、PCA降维、局部敏感哈希（LSH)等，虽然提速了很多，但是作者仍然嫌弃它们慢。而本文提出的PatchMatch算法在寻找最近邻的速度上又是一次质的飞跃（比之前的SOTA还要快1-2个数量级），为那些应用在用户交互场景的实时图像编辑工具提供了强有力的算法支持。说到这里有必要提一句，Photoshop里的content-aware修复工具正是在本文算法的基础上优化集成的。

核心思想：Barnes提出的PatchMatch(PM)算法巧妙利用了图像的局部相关性实现快速块匹配。理解这一点就理解了这个算法灵感的来源。那么，什么叫局部相关性呢？请看下图：

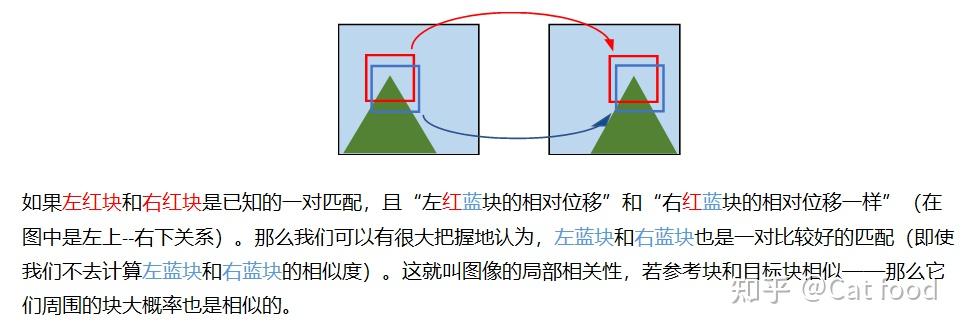
那么，根据这个思想，一旦某个patch有了心仪的匹配，该匹配关系可以迅速传给它的邻居，这样邻居就不用苦苦去寻找匹配了，直接抱大腿就行，从而免去了大量的块匹配计算。相比于之前非常经典的在全局暴力匹配的算法，这是一种很聪明的匹配策略。

2. 研究背景

目前许多研究者发展了一些图像的高级编辑（high-level editing）技术来实现各类需求。这里的高级编辑，指的是让计算机干出一些看起来像人类设计师做出的复杂编辑之类的工作，需要带有一些智能化的色彩，典型的例子比如有：

重构（retargeting）：改变图像的纵横比的同时不会挤压或拉伸图像中有意义的前景物体
修复（completion）：移除不需要的前景并用背景代替；
重组（reshuffling）：移动和重新排列图像里的元素，而且保持plausible

而寻找最近邻匹配在这些高级编辑的任务中往往扮演核心的角色，前面已经提过，现有的最近邻搜索算法在速度上是一个大问题。另外，这些高级编辑也不是全自动的，用户的交互参与也是很重要的，因为：

有时候需要人工干预才能出最好的效果，因为电脑并不知道你想要如何编辑，而只有你自己是清楚的；
有时候甚至连用户自己都不知道想要达到什么样的效果，必须通过不断试错（trial and error），才能逐渐摸索出符合个人判断的最佳效果。

所以，可交互可以说是高级编辑的基本要求，既然要可交互，那么这个算法就得快，要立竿见影，这样才能让用户看到即时效果。针对以上问题，本文提出的PatchMatch算法的核心卖点就是一个字——快。

3. PatchMatch算法

首先需要说明的是，本文算法不保证所有patch都能找到最优匹配，但是可以达到整体上的近似最优，因此作者在文中的用词是近似最近邻搜索（Approximate Nearest-Neighbor Search）。另外需要明确的是：最近邻不是空间位置上的紧挨着，而是特征空间里的距离，在本文中，为patch寻找最近邻实际上就是寻找最相似的块匹配。

在开始之前，我们需要明确作者的一些预设：

下面来详细介绍基于最近邻场（NNF）的快速块匹配算法：

3.1 初始化

初始化就是为最近邻场赋初值，也就是给图A中的每个块随机赋予一个初始的匹配块。赋初值有两类思路：既可以完全赋予随机的初值（匹配肯定是混乱的），也可以加入一些先验的信息（事先指定一部分正确的匹配关系作为先导）。

3.2 迭代

初始化完成后便开始迭代过程，每次迭代都是一个全场扫描过程：奇数次迭代是从上到下逐行扫描，每一行从左到右扫描；偶数此迭代反过来，从下到上，从右到左。扫描的单元是patch，那么每个patch被扫描到时，都要先后地经过两个子过程：匹配传递（propagation）和随机搜索（random search）

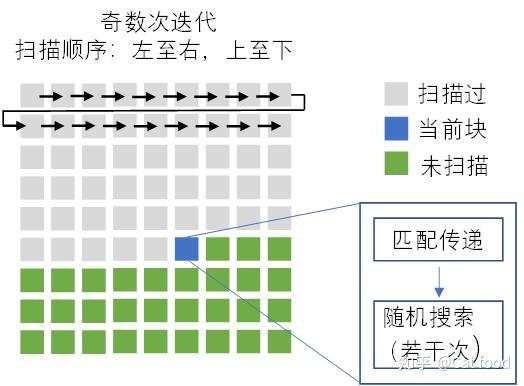
3.2.1 匹配传递（propagation）

匹配传递的思想就是见贤思齐，一个patch会试图借用邻居的匹配关系，看看能不能得到更好的匹配，如果能得到更好的匹配，就果断抄作业，然后丢掉自己的原配。所以说一个学霸patch如果拥有好的匹配成绩，它的offset值是会被它周围的学渣邻居积极学习和借鉴的。具体来说，假设现在在奇数场，正扫描到 (x,y) 处，那么此时这个patch左边的邻居(x-1,y)和上边的邻居(x,y-1)都是已经被扫描过的patch，它们对应的offset值是 f(x−1,y) 和 f(x,y-1) ，这两个值代表这它们在目标图B里匹配块相对于自己的位置。

接下来，当前块会借用左邻居和上邻居的匹配offset值找到两个新的备胎匹配，再算上自己原来的原配，然后比较这三对匹配，看看哪对匹配更好，那么当前块的匹配对象就直接向最优匹配看齐。具体来说，用 D(v) 代表A图中的块(x,y)和B图中的块(x,y)+v之间的匹配误差，那么当前块的offset值f(x,y)就由下式决定：

f(x,y)=argmin_f[D(f(x,y)), D(f(x−1,y)),D(f(x,y−1)) ]

如果还是看不懂这是啥意思，请看下面的解释：

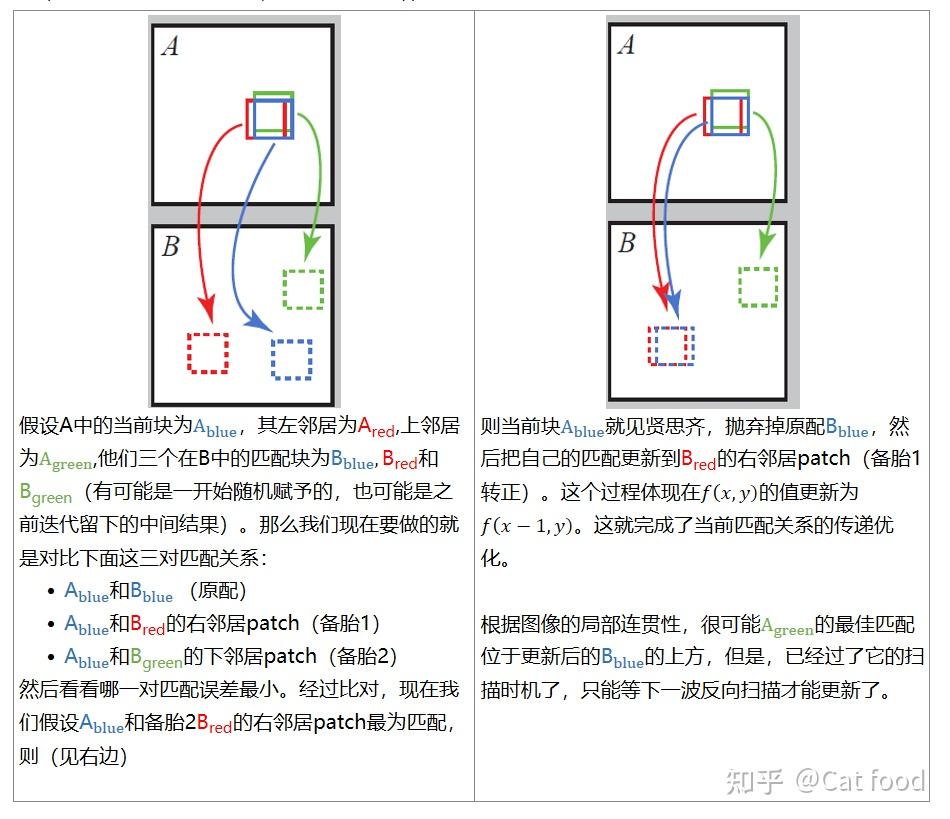
不得不佩服作者的这个设计非常的amazing啊，一旦有patch匹配的还不错，而且处于一致性较好的区域里，那么它会在接下来的扫描中带动其右侧和下侧的邻居们，使他们都获得比较好的匹配，所谓一个人带动了一片。

3.2.2 随机搜索（Random search）

俗话说得好，搏一搏，单车变摩托。当前块 (x,y) 经历了上面所述的传递过程其匹配可能得到了优化，但也许还有进步的空间。作者接下来继续对其施加一个随机搜索的策略，试图通过扰动看看能不能让其跳出局部最优：那就是在以当前块的匹配块(x,y)+f(x,y)为中心，在不断指数衰减的半径区域里随机瞎匹配若干次，直到半径缩到1个像素以下才罢休。

写成数学语言是 \bm{u_i}=f(x,y)+wα^i \bm{R_i}

式中w是最大搜索半径，文中取图像最长边的长度，α是位于0-1之间的固定的指数衰减因子（文中取0.5）， \bm{R_i} 是位于[−1,1]×[−1,1]中服从均匀分布的二维随机数， i 是随机搜索的次数（0,1,2,…），i的递增直到当前搜索半径 wα^i 小于1为止。那么 \bm{u_i } 就是当前块在图B中第i次随机搜索的匹配块的相对位置，如果这几次随机搜索瞎猫碰见死耗子，发现了更好的匹配，那么当前块的匹配关系就随之更新。

当然，作者提出，在这个随机搜索的过程中可以早停，比如正在计算某次随机搜索的匹配误差时，才算到一半就发现已经比原来的值差了，那么再算也没有意义了，此时就可以提前终止了（early termination）。

再次强调，每次迭代都要扫描全图，扫描时每个块都要经过上面所述的传递和随机搜索两个子过程。那么问题来了,迭代多少次合适呢？作者发现，实际上只需4-5次基本上所有的块都能找到心仪的匹配块啦，整个NNF场（就是offset矩阵）基本就收敛了。

4. 一些数学分析

我们假设图A和B是一样大的，各自含有M个像素，然后使用随机的初始化。随机初始化会为每一个源patch分配一个随机的offset以匹配一个随机的目标patch，那么显然，对于某个源patch来说，正确匹配（匹配到最佳目标patch）的概率当然非常非常低，只有1/M。

但是，所谓愚者千虑，必有一得，对于所有的源patch来说，至少有一个正确匹配的概率就很大了（或者说完美避开所有正确答案的概率非常小），很容易算出这个概率是 1−(1−1/M)^M ，当M取较大的值时，这个数字趋近于 1−1/e 。不要小看一个正确的匹配对，通过之前讲过的传递机制可以迅速把它周围一片的错误的匹配关系全都矫正过来。

上面是只有匹配到最好的才算是匹配正确，也就说标准答案是唯一的。但是呢，我们要求其实可以不要这么严格，哪怕匹配到最佳匹配块旁边的几个“次佳”的匹配块也没关系，因为在之前提到的随机搜索环节中，随着搜索圈的逐渐收紧，次佳的匹配关系也很容易被矫正到最佳匹配关系。所以实际上，我们认为匹配到最佳块周围的C个次佳块，也认为是正确匹配。这样一来，至少有一个正确匹配的概率就变成了 1−(1−C/M)^M ，当M取较大的值时，这个数字趋近于 1−e^{−c} ，所以说，看似不靠谱的随机NNF初值，从统计意义上来说，最终收敛的概率还是较大的。