去除纹理的几篇文章学习
去除纹理,其实就是去除噪声。也就是平滑图片的时候尽量保边,即保留结构信息,尽量去除纹理信息,如下图所示:

记录下以下论文:
1. Structure Extraction from Texture via Relative Total Variation, SIGGRAPH Asia 2012
2. Bilateral Texture Filtering, SIGGRAPH 2014
Structure Extraction from Texture via Relative Total Variation
文章提出纹理和结构的区分方式,首先定义一个窗口总变化值,定义如下,其中 \(\partial_x\) 表示 x 方向梯度,\(g\) 表示高斯分布的系数,其实就是窗口内每个像素的梯度绝对值之和:
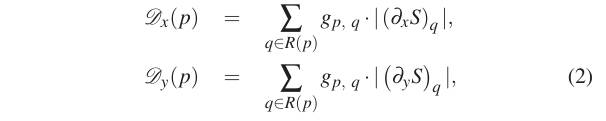
然后新颖的点是,又定一个窗口内部变化值,定义如下,其实就是每个像素的梯度不做绝对值了:
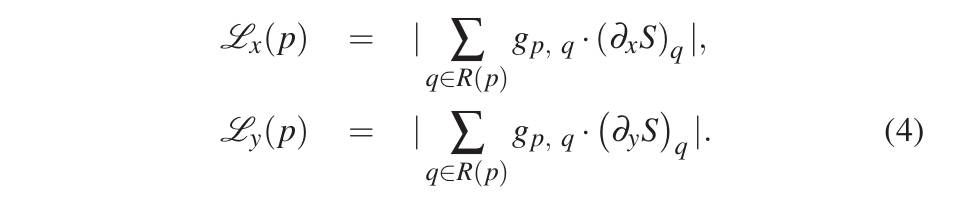
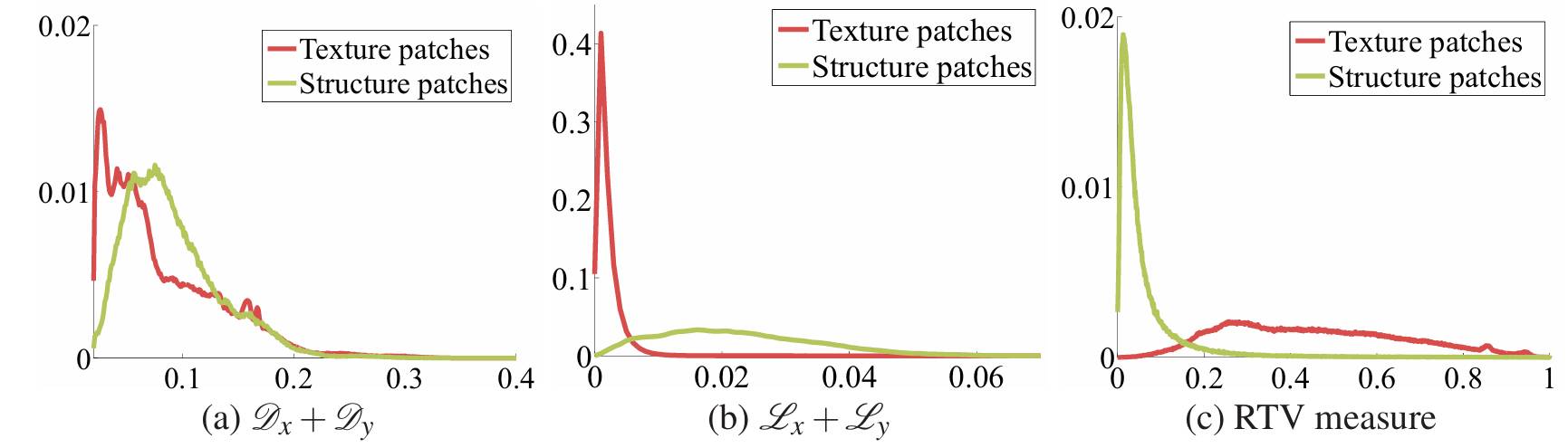
关键发现是:仅包含纹理的窗口中 L 通常小于同时包含结构边缘的窗口中的 L,如下图所示。直观的解释是,局部窗口中的主要边缘比具有复杂图案的纹理贡献了更多相似方向的梯度。说实话,这里完全没懂,也花了很长时间尝试去理解,并且尝试了好多次,但还是没懂。设定一个时间,如果这个时间内不懂就跳过这个,当成定理来看待,不要在这里浪费太多时间!!。
不理解就当成定理!!

然后利用这个发现,进行去噪,最小化公式如下:
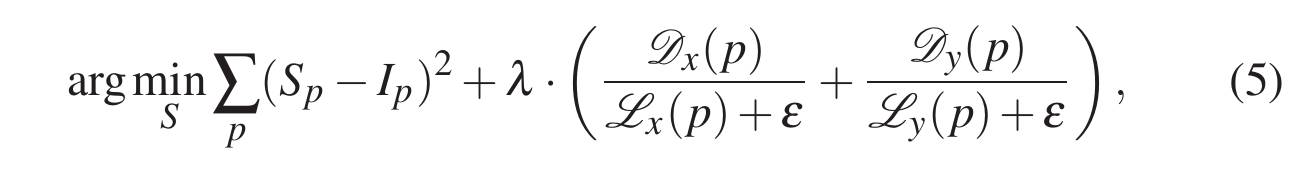
具体从这个公式推出最小化求解,参考论文 3.2 节。上面公式最后一块就是论文提到的 Relative Total Variation(RTV)。
收获: 区别纹理和结构的一个指标 RTV
总结本文,即有一个关键发现是提出了一个窗口内部变化值,其能有效区分纹理和结构。更进一步,提出 RTV 指标(即窗口总变化除以窗口内部变化),其能有效区分纹理和结构。
还是那句话:定好时间尝试理解,但不要花太长时间,如果不能直观感觉为什么这个指标有效,那么就当成定理。下图是论文的实验结果:
Bilateral Texture Filtering
总结一下这篇文章的流程,因为不属于我的方向,所以就快速写一点,还是看原文更好,而且原文写的还可以:
mRTV
第一个,modified RTV,其实就是利用上文的 RTV 指标,进行了一些修改。其中 \(\Omega_q\) 是以像素 \(q\) 为中心的窗口,\(\partial I\) 是标准的梯度大小计算。
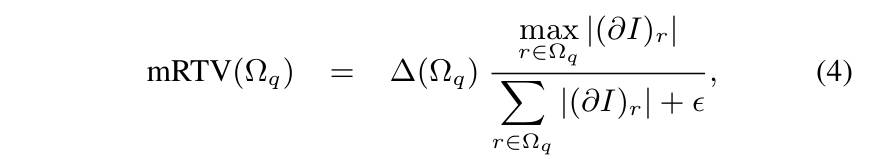
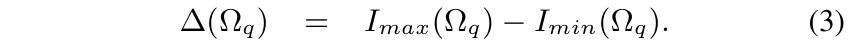
作者就是说在平滑区域中,mRTV(多尺度相对总变差)值倾向于非常小。在包含少数边缘的结构块中,mRTV 值相对较大,而在具有频繁振荡的纹理块中,mRTV 值则相对较小。
至于为啥,就不详细去了解了。如果不是这个方向的人,感觉可以直接当成定理看待吧。也希望能有人帮忙直观解释一下。
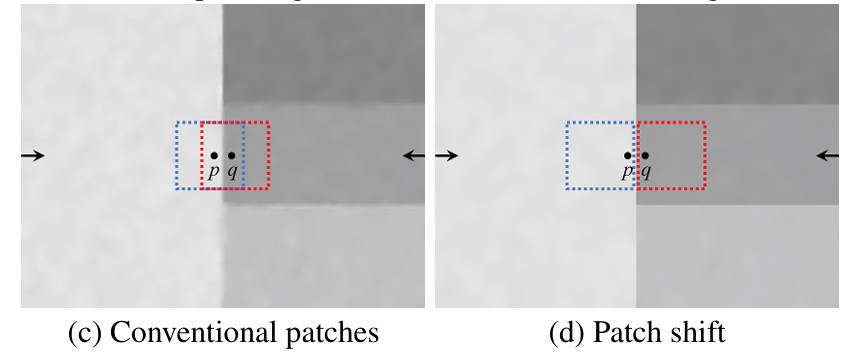
Patch Shifted
第二个,作者提出去噪的时候用一种 Patch Shifted 方式,如下图,即如果像素点是结构边缘,那么就在其附近中一个平坦的点,用那个点为中心的窗口来代替:
mRTV + Patch Shifted
前面提到 mRTV 在平坦区域值小,所以 Patch Shifted 找附近平坦的点,那么就用 mRTV 来作为指导去找平坦点。
但是作者提到 mRTV 在平坦区域虽然小,但对噪声很敏感。作者提了一个场景:一个平滑区域,强度逐渐变化(即类似灰卡)。此时某个点加入是噪点,那么做 Patched Shifted 发现它的 mRTV 很大,所以会用附近平坦点的窗口。但区域是平滑变化的,所以这个噪点最后恢复后还是会和周围点格格不入。
因此作者就提到,不应该完全依赖 Patch Shifted 后的窗口,也要考虑原窗口,即加权求和。如下图公式,G 是 Patch Shifted 后的窗口,B 是原窗口(其实也不是原窗口,图片一开始会做高斯模糊,具体看下面算法流程)。
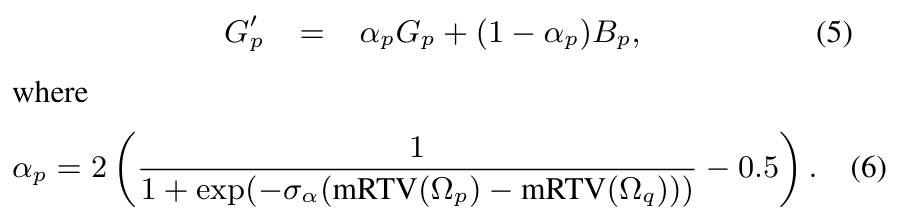
上面的公式中如果 p 的 mRTV 比 q 越大,那么就越会使用 q 窗口进行平滑。其实这里感觉还是没有解决上面的平滑过渡例子,不是很理解。
算法流程
算法流程如下,感觉很清晰,其中 Joint Bilateral Filter 忽略掉,就当成一种去噪方法就行。
