梯度投影融合闪光非闪光

用梯度投影融合闪光非闪光，来自 Wang Hawk 老师在深蓝学院开设的《计算摄影学进阶》课程第五章，质量蛮好的。

现在有同一场景的闪光和非闪光图片，目标是合并，既可以有闪光图片的低噪声，也能避免在闪光图片的高光。是代码我自己实现了，放在 code 目录中。

写给我自己：看录制的视频，很快就能看懂。

解决痛点

闪光非闪光融合有一个用联合双边滤波进行融合的方法（个人笔记），但是这个方法很显著的缺点是：

有的时候闪光和非闪光可能有反射现象，这个时候应该丢掉其中之一，但是联合双边滤波的方法无法做到这一点。比如第一张图时闪光有反射，第二张图时无闪光有反射。

引入梯度解决反射

作者认为，梯度可以帮我们解决反射问题。

非强反射区域，闪光和非闪光梯度应该相似；相反，在强反射区域，闪光和非闪光梯度方向不同。

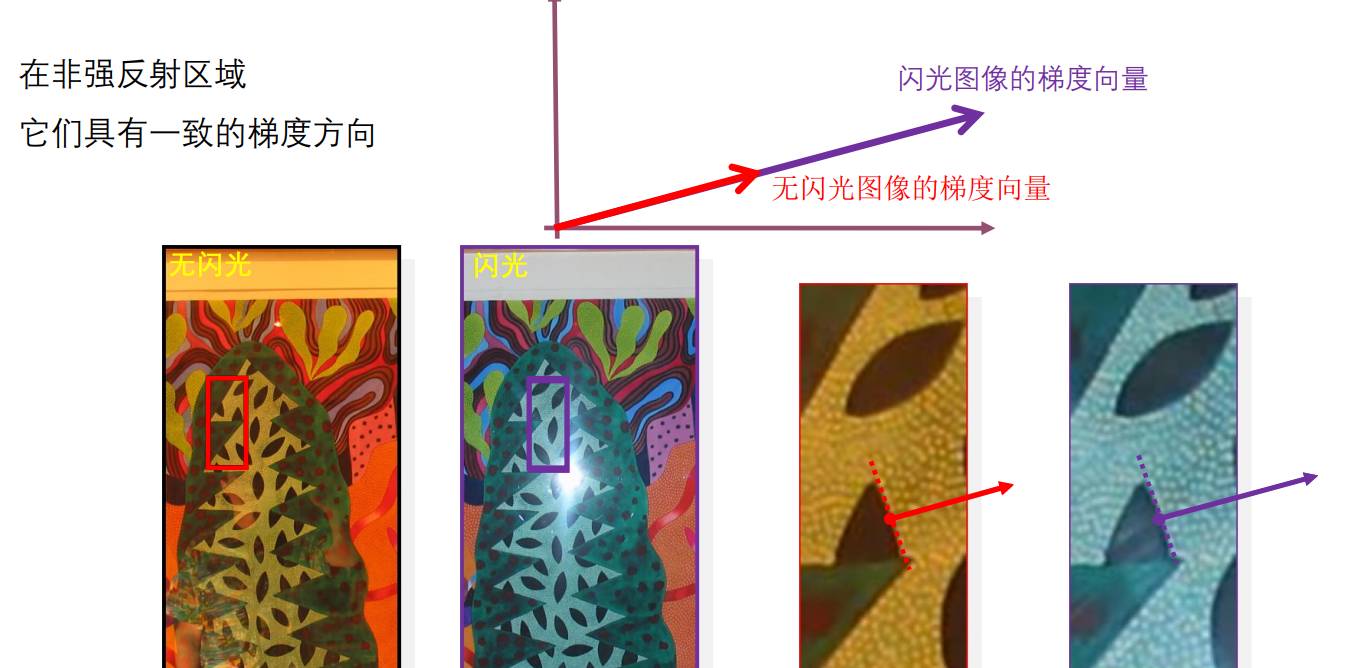
此时用梯度投影就能够消除反射，如果闪光有反射，那就闪光映射到非闪光，反之亦然。

算法细节

我们拿到两张图片后，计算各自的梯度。如上面所述，在非反射区域，梯度一致，此时更加相信闪光图；在反射区域，则更加相信非闪光图。

首先计算梯度的相关程度，如下所示：

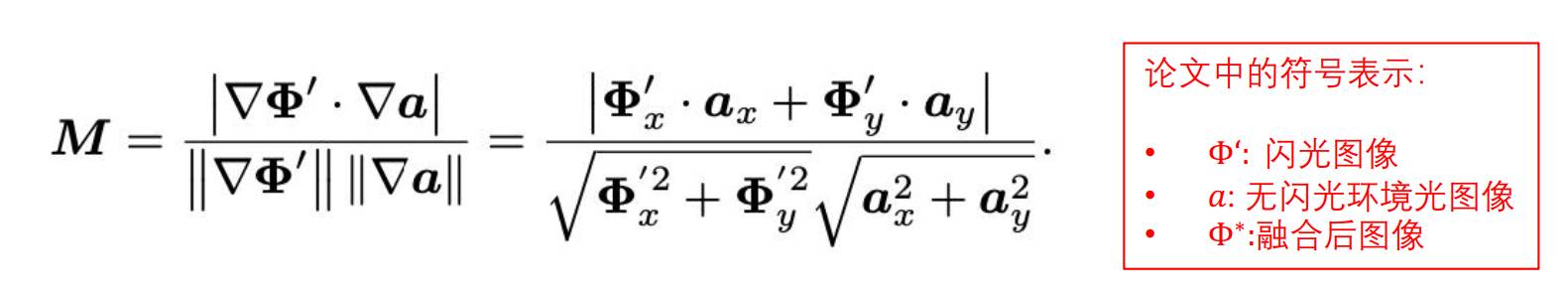
然后利用这种相关程度做一个加权求和，即越不相关我们就越信任非闪光图片的梯度：

\[ \nabla \Phi^{*} = M *\nabla \Phi^{'} + (1 - M) * \nabla \alpha \]

但是还有一个问题：闪光图像容易有过曝的亮点，在这种地方的新的梯度会非常不准确。所以此时我们更信任原始的非闪光梯度。所以还是做一个加权求和，需要用检测闪光图像的亮度进行求权重：

\[ w_s(x, y) = \tanh(\sigma * (I(x, y) - \tau_s)) \]

论文中 \(\sigma = 40\)，\(\tau_s = 0.9\)，需要对 \(I\) 先归一化，最后算出权重后也要归一化以下，最终图像如下：

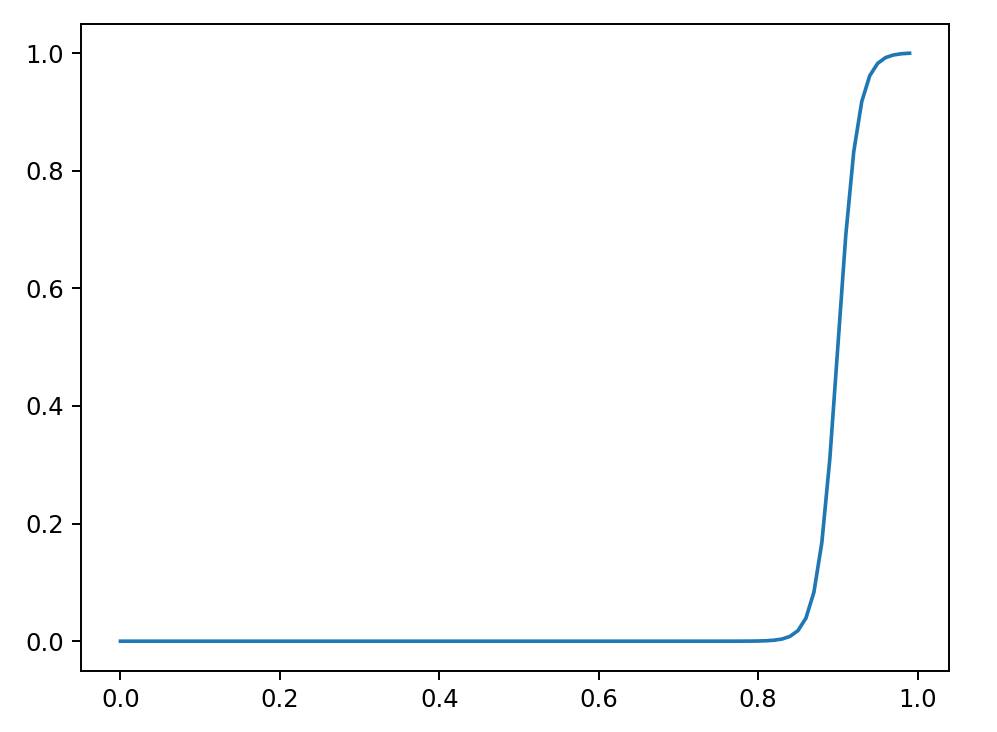
相当于越亮的地方，我们就越信任原始的非闪光梯度，所以最后我们得到的梯度为：

\[ \nabla \Phi^{*} = w_s * \nabla \alpha + (1 - w_s) * \nabla \Phi^{*} \]

得到新的梯度后，需要还原图像。这儿其实是一个经典问题，把它当成泊松融合就行：即我们有要融合的图像，这是未知的，和泊松融合一样；我们还有一个原始图像，这里的区别就是：泊松融合那里这个是知道的，但我们这里只知道它的梯度场。

但没有关系，泊松融合的经典公式如下，其中 \(f\) 是最终融合后的图像，\(\bold{v}\) 是融合前图像的梯度场，\(\Omega\) 是融合区域（不包含边界），\(\partial \Omega\) 是融合区域边界。

对于 \(\text{div } \bold{v}\)，其表示对原始图像的梯度场 \(v\) 做散度，因此就是拉普拉斯操作（下面的 \(g\) 是原始图像）：

\[ \text{div } \bold{v} = \text{div} (u, v) = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \]

\[ (u, v) = \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right) \Rightarrow \text{div } \bold{v} = \frac{\partial^2 g}{\partial x^2} + \frac{\partial^2 g}{\partial y^2} \]

而我们上面一大段操作得到的新的梯度场，就是这里的 \(\bold{v}\)，即这里的 \(u\) 和 \(v\)。所以 \(\text{div } \bold{v}\) 就用上面的第一行的公式即可得到，即梯度 \(u\) 和 \(v\) 分别再做一次行或列的梯度，然后加起来。

之后用泊松融合的公式去求解，其中边界的值就规定是非闪光的图像边界即可。

结果：

其他说明

上面一章中是加权融合闪光非闪光的投影，原论文中也提到有直接投影的，如下面的公式：

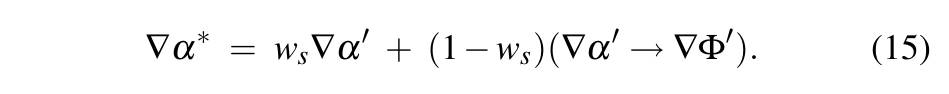
这个就是非闪光可能有反射，所以直接一股脑把梯度投影到闪光图上。似乎对于发生反射现象而言，这种做法更好。没有反射现象时，用上一章的加权融合更好。

Comments