边缘检测方法:LSD
介绍一种边缘检测方法:LSD,来自以下文章,它可以在 OpenCV 中使用,具体用法在另一篇笔记中。
- LSD: a Line Segment Detector
首先是总体逻辑先过一遍,先不纠结各个步骤具体是如何做的。
总体流程
流程一:先对图像求梯度,得到方向,然后把大致接近的方向组合在一起。如下图所示(先不纠结如何实现),便于讲述,每一组叫做 Line Support Region。
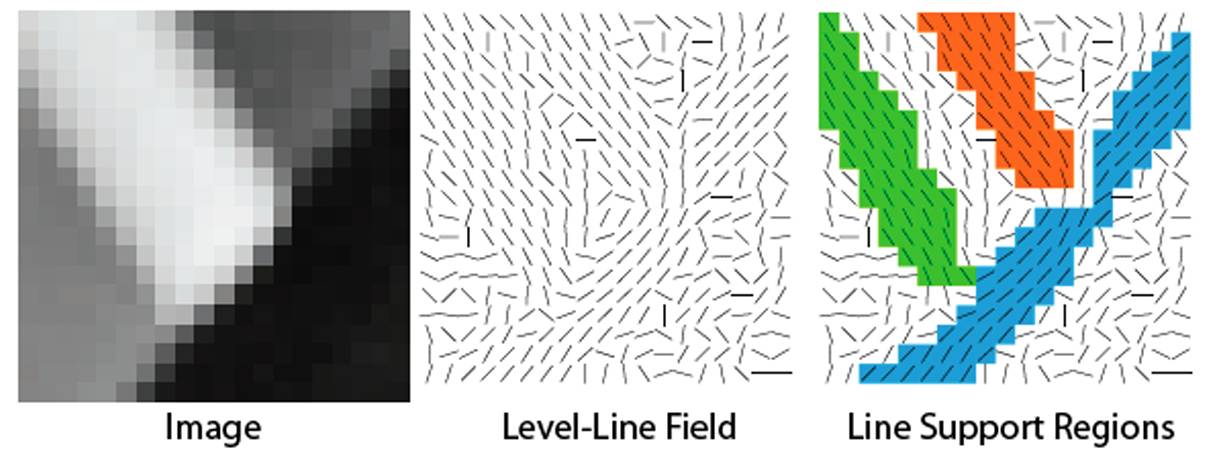
流程二:然后对每个组合求一个最小外接矩形,看看里面的点有多少是和矩形的方向一致的,比如下图,就只有 8 个点是和矩形的方向一致的,这些点叫做 aligned points。
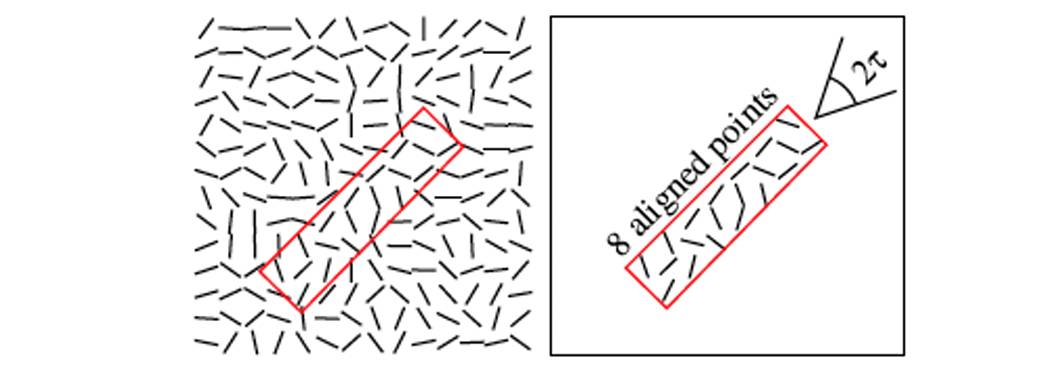
流程三:判断上面说的符合矩形方向的点数量够不够,即这个矩形是否可以作为最终直线。
流程四:如果不够则把矩形删掉一个点,继续上述操作。
流程一:求解 Line Support Region
每个点梯度计算,有大小和方向。梯度小的点往往出现在平滑区域,或者仅仅是噪声。即不是我们想要的直线,为了避免干扰,梯度值小于 \(\rho\) 的像素会被标记,不参与后面的计算。
然后开始依次遍历那些未标记的点,遍历顺序是梯度从大到小,其中作者用的桶排序,也符合常规做法。
假设现在从像素点 \(p\) 开始找新的 Line Support Region,先计算 \(p\) 的八联通这个八个点的梯度方向是否和 当前 Line Support Region 的方向 在容忍度 \(\tau\) 内,其中论文中 \(\tau = 22.5 \degree = \pi / 8\)。
当前 Line Support Region 的方向计算如下,即把里面的像素点各自 \(\sin\) 和 \(\cos\) 求和,然后求 \(\arctan\)。
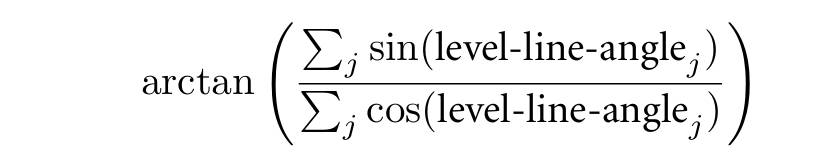
如果符合条件,就加入那个点,并且做一个标记,然后重复上面步骤。
流程二:求解最小矩形及其 aligned points 数量
求最小外接矩形这是经典问题,这里不赘述。这里快速提一下,如下图是矩阵中心:
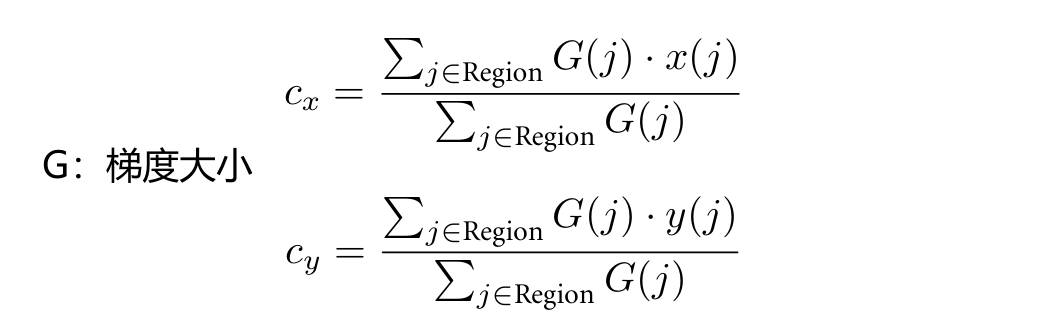
这个矩形的方向则是用轮廓的矩,求下面的矩阵的最小特征值对应的特征向量,就是矩形的方向:
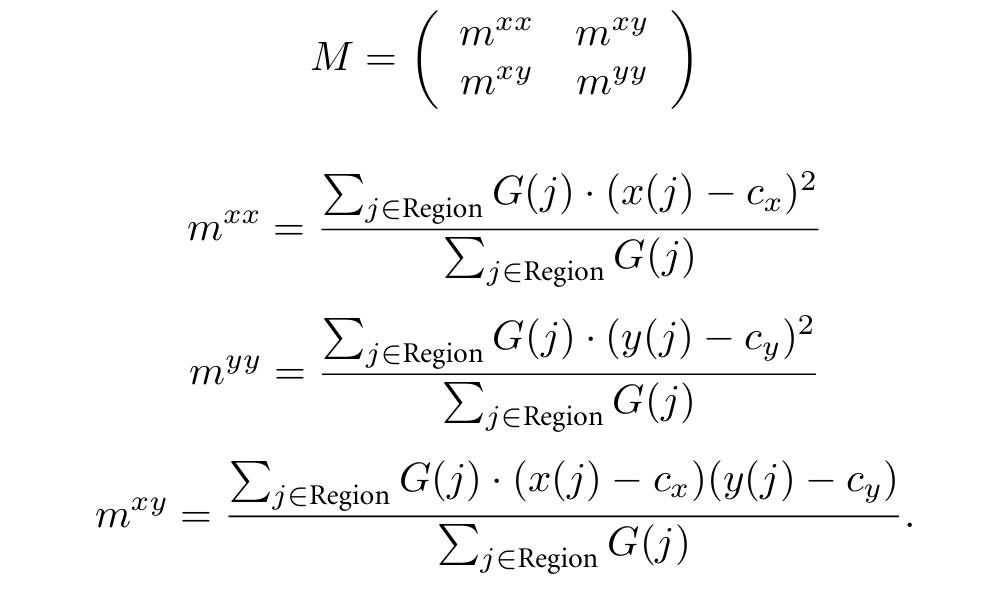
然后 aligned points 数量也很朴素:遍历比较呗,比较当前遍历的点的梯度方向和上面的矩形方向是否在容忍度 \(\tau\) 内。
虽然我们在流程一中加入点的时候,考虑的容忍度也是 \(\tau\),但是这里比较的是最终矩形的方向,而不是流程一中逐渐更新的 Line Support Region 的方向(流程一中用 \(\arctan\) 计算的公式)。
流程三:判断矩形是否可以作为最终直线
作者用了一个叫做 NFA 的指标,这个指标在另一个方法 EDLines 中也会用到。
NFA, the Number of False Alarms,假阳性率,计算公式如下:
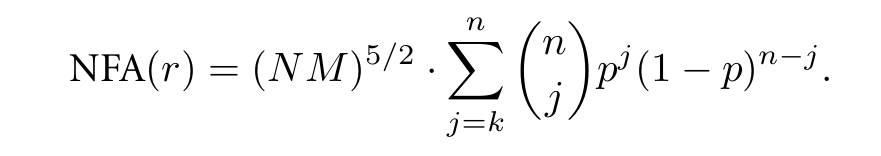
其中 \(N\) 和 \(M\) 是图片的大小,\(n\) 是当前矩形的像素数量,\(p\) 叫做精确度,默认值设为 \(\tau / \pi\),\(k\) 是符合条件的像素点数量,而这个条件阈值就是 \(p\pi\)。
这个方法也叫做 Helmholtz principle,从上面公式也能看出是否能作为最终直线甚至和图像大小有关系。确实,同样长度的直线,在小图中可作为直线,但大图中可能还是偏短。
最后如果 \(NFA(r) \leq \epsilon\),则认为这个矩形可以作为最终直线。论文中参数 \(\epsilon = 1\)。其参考了 2008 年的一篇文章:From Gestalt Theory to Image Analysis。
流程三番外:进一步判断矩形是否可以作为最终直线
作者提出用 NFA 进行评估有一个问题,如下图所示,如果前半部分是一个合理误差内的方向,后半部分是另一个相反的合理误差方向,最后会通过 NFA 检测:

然后作者就提出进一步判断,用符合常规的数量占比来判断,如下图所示,论文使用的阈值是 \(D = 0.7\),即需要 \(d > 0.7\)。但说实话我感觉好像还是没有解决问题啊,暂时跳过去吧,这些都是细节中的细节,实在不行看 OpenCV 源码...
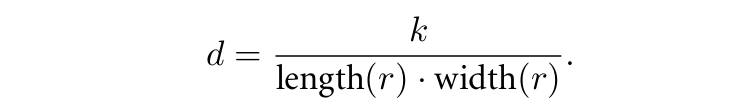
流程四:不符条件则分割矩形
如果矩阵不符合要求,则按照如下步骤进行,一旦有一个步骤发现 NFA 值满足要求,那么就停止:缩小精确度 \(p\)、减小矩形宽度、减小矩形一边的长度、减小另一边的程度、进一步缩小精确度 \(p\)。

如果最后矩形过小也会被丢弃。