Piecewise linear 快速双边滤波记录
原始论文:Fast Bilateral Filtering for the Display of High-Dynamic-Range Images
双边滤波:

假设窗口是 \(k*k\),图像大小是 \(n*n\),那么双边滤波的计算量是多少?只算乘法,需要 \(n^2*k^2*2\) 次,\(k\) 如果很大那计算量太大了。
上面这篇文章就提了一个有趣的思路。想了半天终于明白本质原因了,下面记录一下我的理解。
加速,那就空间换时间呗。假设我们有无限大的容量,有什么好的方法加速呢?提前算好,最后直接查表呗。
但是怎么提前算好,直接给出答案。看如下的公式,其中 \(i^j\) 表示 0-255 内的数。也就是我假定某个像素大小是 \(i^j\),提前算好。到最后查表即可。

但是上面这个式子和原始有什么改进?可以使用分离滤波!它的步骤如下:
1. 遍历 \(i^j\) 从 0 到 255,下面讲解每次遍历的情况。
2. 每个像素算出 \(g(I_p-i^j)\),即最后得到 \(n*n\) 的 \(G\) 表,其中 \(G(x,y)\) 的含义是:如果双边滤波某个像素大小是 \(i^j\),计算双边滤波时的窗口中有 \((x,y)\) 点,\(G(x,y)\) 表示和它在值域上的差距
3. 上图中第二个公式,相当于对 \(G\) 表做高斯滤波,这个是可以优化的,经典的方式是拆分为一维。这样能得到 \(n*n\) 的 \(k\) 表,其中 \(k(x,y)\) 的含义是:如果 \((x,y)\) 像素大小是 \(i^j\),那么以它为中心,计算朴素双边滤波时的权重和
4. 上图中第一个公式,\(G\) 表和 \(I\) 表对应相乘,得到 \(H\) 表,同样得到 \(H\) 后再做高斯滤波,速度很快,得到 \(J\) 表
5. 最后 \(J\) 除以 \(k\),就得到这次遍历的值
算下来,需要多少乘法?高斯滤波是可以分解为两个一维高斯核相乘,\(n*n\) 需要 \(2n\) 次乘法。计算 \(G\) 不需要乘法,直接查 \(g\) 表;计算 \(k\) 需要 \(2k*n^2\) 次乘法;计算 \(H\) 需要 \(n^2\);计算 \(J\) 需要 \(2k*n^2\) 次乘法。
由于从 0 到 255 遍历,总结下来,需要 \(256*n^2*(4k+1)\) 次乘法。原始朴素的,需要 \(n^2*k^2*2\) 次乘法。当 \(k\) 变大时,优化会很显著。
深入思考
究竟优化在哪里了?想了半天,终于明白:每次遍历我是认为中心点一样的值,这样能够复用一些结果!
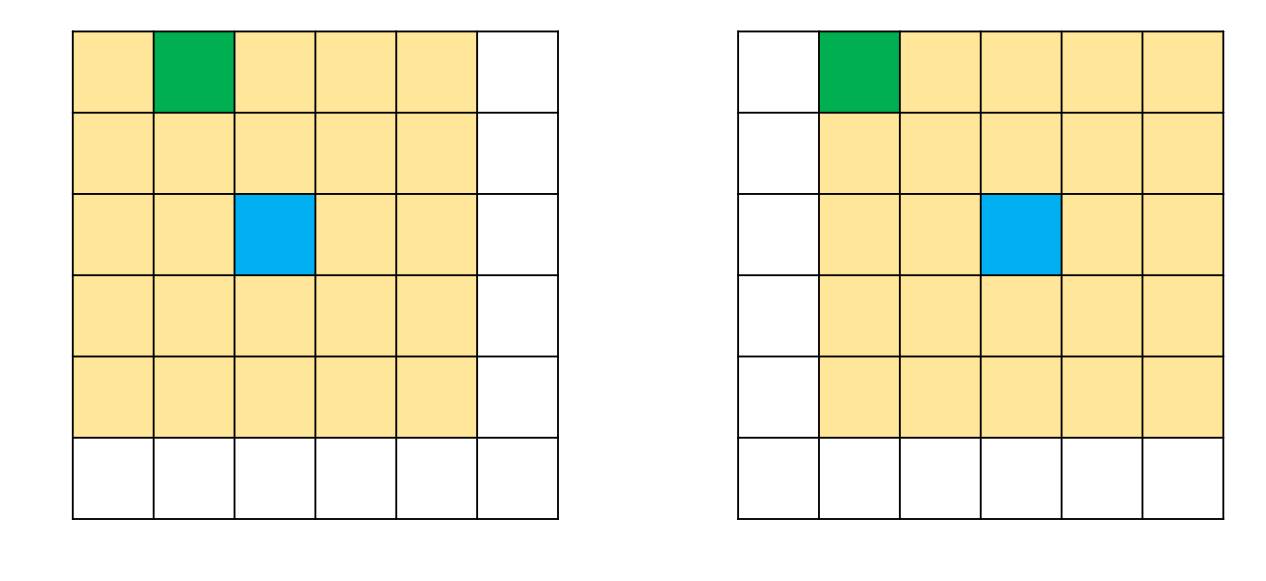
如图,由于每次按照像素值遍历的,即假设我遍历到 10,此时想要的:假定蓝一是 10,算一下双边滤波它最后多少;假定蓝二是 10,算一下双边滤波它最后多少。
带来什么好处?绿色的点,虽然处理以不同像素为中心的窗口,它的 \(g\) 值始终是一样的!这样有什么好处?不需要重复计算了!
朴素的双边滤波每个窗口是独立的,需要重复计算绿色点的 \(g\) 值,然后才能再 \(g*f\),再 \(g*f*I\)。
现在这样,我们每个点的 \(g\) 值处理不同窗口都是一样,即我们最后可以得到一个同等 \(n*n\) 的 \(G\) 表,那么 \(g*f\) 可以直接高斯滤波了!可拆成两个一维了!非常精妙!
额外补充
当然我们空间不是无限大,我们做不到从 0 遍历到 255。论文中进行了分段,即 0、16、32... 这样,最后插值即可。