Skip to content

二维几何和轮廓

来自本人笔记: https://github.com/masterAllen/LearnOpenCV/blob/main/docs/二维几何和轮廓

函数说明：

最重要的是记住，这里的函数基本都是纵坐标在前、横坐标在后！！

基础函数：寻找轮廓、近似轮廓；OpenCV 本身的文档就很不错：链接

处理一堆点时的函数：在 dealwith_points.ipynb 文件中有详细使用

  • 要求点集必须是轮廓:
功能 函数名称
轮廓周长 arcLength
轮廓面积 contourArea
轮廓的矩 moment, HuMoment
检测轮廓是否是凸集 isContourConvex
判断某个点是否在轮廓以内 pointPolygonTest(measureDist=False)
判断某个点到轮廓的距离 pointPolygonTest(measureDist=True)
  • 点集不一定构成轮廓（当然如果是轮廓也能用）:
功能 函数名称
包围点集的最小矩形（正方向） boundingRect
包围点集的最小矩形（任意方向） minAreaRect + boxPoints
包围点集的凸包 convexHull
包围点集的椭圆 fitEllipse, fitEllipseAMS, fitEllipseDirect
包围点集的圆 minEnclosingCircle
点集模拟的线 fitLine
  • 处理两个轮廓:
功能 函数名称
寻找两个轮廓的交集（必须是凸多边形） intersectConvexConvex
寻找两个矩形的交集（和上面的区别见具体细节） rotatedRectangleIntersection
  • 匹配和变换两个轮廓，具体请查阅 1.8节的记录：
功能 函数名称
比较两个轮廓一 matchShapes
比较两个轮廓二 ShapeDistanceExtractor
比较两个轮廓三 HistogramCostExtractor
变换轮廓 ShapeTransformer

其他杂项：

  • convextiyDefects: 凸包缺陷检测
  • connectedComponents, connectComponentsWithStats: 连通域相关的函数

具体细节

大部分函数的实现都在 find_contours 和 dealwith_points.ipynb 文件中，没有的也都是很简单纯粹的函数，下面是几个还需要再讲讲的函数。

findContoursLinksRuns

官方文档写的就不错，而且这个函数不用啥参数，直接就是一张图片就行：

1721109275885

moments, HuMoments

什么是 moments，这篇文章 和 这篇文章 讲的非常不错，用法也直接参考第一篇文章就行。

简单而言，moments 叫做矩，两个作用：可以用来求轮廓质心、求 HuMoments；而 HuMoments 则是图像的 Hu 不变矩，是指目标具有旋转、缩放不变性，即目标的 Hu 不变矩不会随其大小、方向变化而变化。

RotatedRect 类型

1721125583653

Python 中默认把函数返回的 RotatedRect 类型作为 tuple，而有时需要利用 RotatedRect 的方法。返回的方式为 (center, size, angle)，所以只要用构造方法即可:

# 获取 rotatedRect 的点
point_set = np.array([[20, 20], [20, 13], [28, 19], [33, 18], [17, 31]])
rect1 = cv2.minAreaRect(point_set)
points1 = cv2.RotatedRect(*rect1).points()

rotateRectangleIntersection

和 intersectConvexConvex 的区别就在于，rotate 输入的是 RotatedRect 类型，intersect 输入的是轮廓。如果两个都是 rotatedRect，那就用前者；否则就用后面。

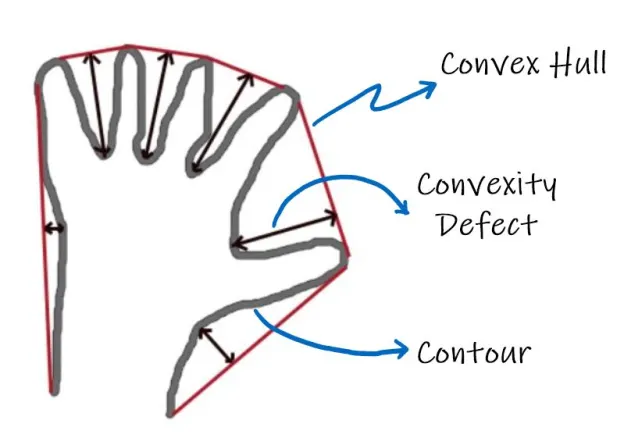
convextiyDefect

凸包缺陷检测，即传入轮廓和凸包，得到凸包和轮廓之间的间隙，参考这篇文章，写的极好，他的图片介绍也很好：

1721127173146

connectedComponents

这篇文章写的极好，本身函数没有太大的坑点，只要知道这是负责得到图片的各个连通域的。后续可以用这些连通域进行分割等操作。

Comments